2015-05-13
774
Информационная матрица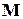 
ортогонального ЦКП имеет вид
,
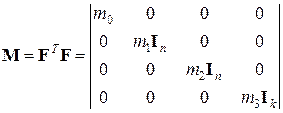где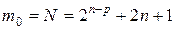 
; 
;
; 
;
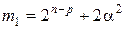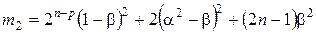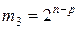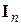– единичная матрица размером 
; 
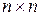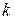– число сочетаний из 
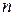по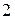 
.
Соответственно дисперсионная матрица
,
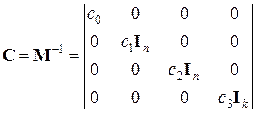где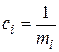 
. Значения 
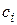для некоторых 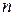приведены в табл. 2.2.
Тогда соотношения для расчета оценок регрессионных коэффициентов имеют вид
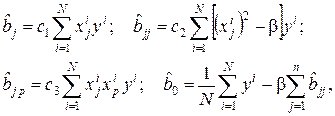
где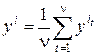 
; 
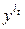– значение исследуемой переменной 
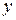в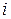 
-й точке плана при 
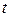-м параллельном опыте.
Однако при использовании ПЭВМ целесообразнее использовать матричное представление, когда расчет оценок регрессионных коэффициентов осуществляется в виде
,
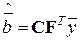где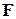 
– матрица планирования эксперимента; 
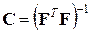– дисперсионная матрица; 
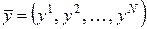– вектор средних значений наблюдений в точках факторного пространства.
Оценки дисперсий полученных коэффициентов регрессии определяются выражениями:
– для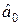 
: 
;
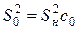– для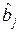 
: 
, 
;
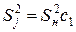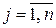– для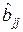 
: 
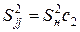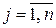, ; (2.3)
– для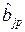 
: 
, , 
;
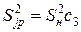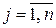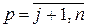– для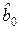 
: 
,
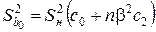где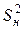 
– дисперсия ошибок наблюдений.
Гипотеза о статистической значимости (отличии от нуля) коэффициентов регрессии проверяется критерием Стьюдента.
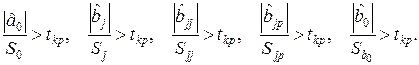(2.4)
Критическое значение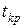 
критерия находят из таблицы распределения Стьюдента по числу степеней свободы 
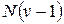и уровню значимости 
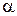(прил. 2).
Если неравенство выполняется, то гипотеза о значимости коэффициента принимается, в противном случае коэффициент считается незначимым и приравнивается к нулю.
|
|
|
Так как все коэффициенты оцениваются независимо, то изменение оценки любого коэффициента (например, исключение соответствующего члена из уравнения) не приводит к изменению других оценок и их дисперсий. Исключение составляет коэффициент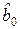 
, т. к. он связан с оценками при квадратах переменных, поэтому исключение квадратичных членов приводит к изменению 
.
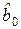Необходимо помнить, что незначимость коэффициента может быть обусловлена и неверным выбором интервала варьирования фактора. Поэтому иногда бывает полезным расширить интервал варьирования и провести новый эксперимент.
