При рототабельном ЦКП нормирование масштабов факторов, порядок постановки опытов, проверка воспроизводимости опытов производятся так же, как и при ортогональном ЦКП. Несколько отличаются только выражения для расчета оценок коэффициентов регрессионного уравнения и их дисперсий.
Информационная матрица 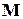 рототабельного ЦКП близка к диагональной
рототабельного ЦКП близка к диагональной
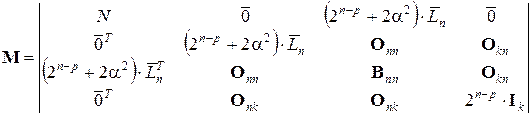 ,
,
где 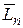 – вектор-строка размерности
– вектор-строка размерности 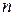 , все элементы которого единичные;
, все элементы которого единичные;
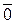 – вектор-строка размерности
– вектор-строка размерности 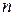 , все элементы которого нулевые;
, все элементы которого нулевые; 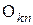 – матрица размером
– матрица размером 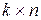 элементов, все элементы которой нулевые;
элементов, все элементы которой нулевые; 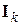 – единичная матрица размером
– единичная матрица размером 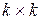 ;
; 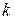 – число сочетаний из
– число сочетаний из 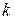 по
по 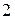 ;
;
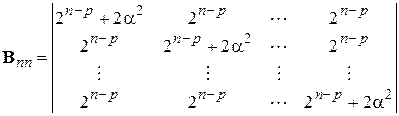 .
.
Оценки коэффициентов можно рассчитать, используя следующие соотношения:
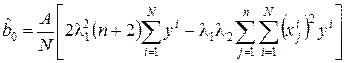 ;
;
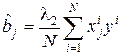 ; (3.1)
; (3.1)
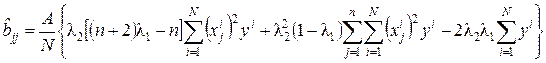 ;
;
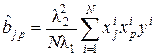 ,
,
где 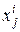 – значение переменной
– значение переменной 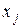 в
в 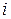 -й точке факторного плана;
-й точке факторного плана;
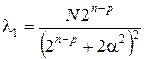 ;
; 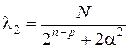 ;
; 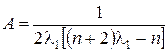 ;
; 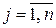 ;
; 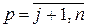 .
.
Однако расчет по формулам (3.1) является громоздким, рациональнее использовать матричное представление, когда расчет оценок регрессионных коэффициентов осуществляется в виде
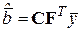 ,
,
где 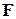 – матрица планирования эксперимента,
– матрица планирования эксперимента, 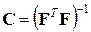 –дисперсионная матрица,
–дисперсионная матрица, 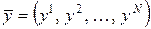 – вектор средних значений.
– вектор средних значений.
Для оценки дисперсий оценок коэффициентов регрессии можно использовать соотношения:
– для 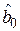 :
: 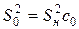 ;
;
– для 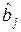 :
: 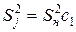 ;
;
– для 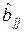 :
: 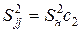 ; (3.2)
; (3.2)
– для 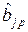 :
: 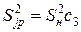 ,
,
где 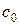 – диагональный элемент дисперсионной матрицы, соответствующий свободному члену ММ;
– диагональный элемент дисперсионной матрицы, соответствующий свободному члену ММ; 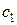 ,
, 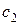 ,
, 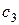 – диагональные элементы дисперсионной матрицы, соответствующие соответственно линейным членам, квадратичным членам и взаимодействиям математической модели;
– диагональные элементы дисперсионной матрицы, соответствующие соответственно линейным членам, квадратичным членам и взаимодействиям математической модели; 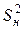 – оценка дисперсии наблюдений, определяемая соотношением (3.4).
– оценка дисперсии наблюдений, определяемая соотношением (3.4).
При оценке статистической значимости коэффициентов регрессии по критерию Стьюдента необходимо учесть, что условие значимости имеет вид
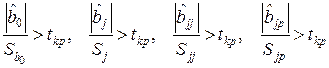 . (3.3)
. (3.3)
Критическое значение критерия 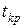 находят из таблицы распределения Стьюдента по числу степеней свободы и уровню значимости
находят из таблицы распределения Стьюдента по числу степеней свободы и уровню значимости 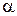 (прил. 2). Если неравенство выполняется, то гипотеза о значимости коэффициента принимается, в противном случае коэффициент считается незначимым и приравнивается к нулю.
(прил. 2). Если неравенство выполняется, то гипотеза о значимости коэффициента принимается, в противном случае коэффициент считается незначимым и приравнивается к нулю.
Необходимо помнить, что при рототабельном ЦКП оценки коэффициентов при линейных членах и парных взаимодействиях некоррелированы с оценками остальных коэффициентов, а при квадратичных членах – коррелированы между собой и оценкой свободного члена. То есть вывод о статистической значимости коэффициентов при линейных членах и взаимодействиях можно делать независимо от значений остальных коэффициентов. Исключение любого из квадратичных членов приводит к изменению оценок остальных, а также оценки свободного члена 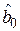 .
.
Адекватность ММ проверяется по F-критерию Фишера. Его расчетное значение определяется соотношением (1.5)
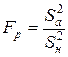 .
.
Если эксперимент повторяется 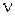 раз в каждой точке плана, то оценку дисперсии ошибок наблюдений
раз в каждой точке плана, то оценку дисперсии ошибок наблюдений 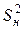 можно найти по формуле
можно найти по формуле
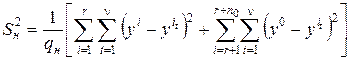 , (3.4)
, (3.4)
где 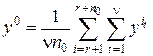 ;
; 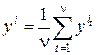 ;
; 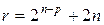 ;
;
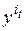 – значение зависимой переменной в
– значение зависимой переменной в 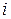 -й точке плана при
-й точке плана при 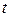 -м параллельном опыте;
-м параллельном опыте;
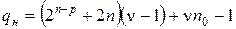 – число степеней свободы.
– число степеней свободы.
Оценка дисперсии неадекватности 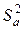 определяется выражением
определяется выражением
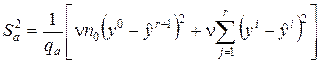 ,
,
где 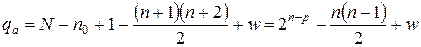 – число степеней свободы;
– число степеней свободы; 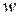 – число незначимых коэффициентов регрессии.
– число незначимых коэффициентов регрессии.
Если 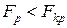 , то модель считается адекватной при выбранном уровне значимости
, то модель считается адекватной при выбранном уровне значимости 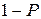 , где
, где 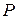 – доверительная вероятность.
– доверительная вероятность.
Для записи ММ в реальных физических величинах производят обратный переход от стандартизованного масштаба к натуральному. Это можно сделать, использовав соотношение (2.1). После чего записывают окончательный вид модели.
3.3. Пример расчета рототабельного центрального
композиционного плана
Пусть при трех сериях опытов с помощью рототабельного центрального композиционного эксперимента требуется исследовать влияние производственных факторов (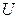 – опорное напряжение
– опорное напряжение 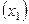 ,
, 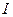 – ток потребления
– ток потребления 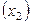 ,
, 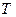 – конечная температура нагрева
– конечная температура нагрева 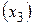 ) на качество производства магнитных дисков. Номинальные значения факторов:
) на качество производства магнитных дисков. Номинальные значения факторов: 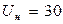 В,
В, 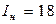 А,
А, 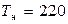
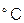 .
.
Условия проведения опытов сведем в табл. 3.3 и проведем нормализацию масштабов факторов.
Таблица 3.3
Условия проведения опытов при рототабельном ЦКП эксперимента
| Характеристика плана | Натуральный масштаб | Нормиро-ванный
масштаб 
| ||
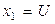 , В , В
| 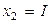 , А , А
| 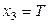 , , 
| ||
| Нулевой уровень | ||||
| Верхний уровень | +1 | |||
| Нижний уровень | –1 | |||
| Звездные точки | 35,046 | 21,364 | 253,64 | +1,682 |
| 24,954 | 14,636 | 186,36 | –1, 682 |
Cоставим МП эксперимента, в соответствии с которой проведем рандомизированные опыты. Полученные результаты запишем в табл. 3.4, где 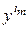 – численные значения исследуемого параметра,
– численные значения исследуемого параметра, 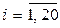 – номер точки в факторном пространстве,
– номер точки в факторном пространстве,
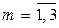 – номер параллельного опыта. В эту же таблицу будем записывать и другие получаемые результаты.
– номер параллельного опыта. В эту же таблицу будем записывать и другие получаемые результаты.
Проведем статистическую обработку полученных результатов. Для проверки воспроизводимости опытов по критерию Кохрена (2.2) при выбранном уровне значимости 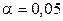 вычислим в каждой точке факторного пространства среднее значение
вычислим в каждой точке факторного пространства среднее значение
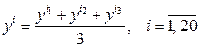
и оценку дисперсии наблюдений исследуемого параметра
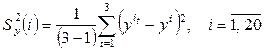 .
.
Рассчитаем оценки коэффициентов регрессионного уравнения. Для этого составим матрицу  :
:

Находим дисперсионную матрицу  :
:
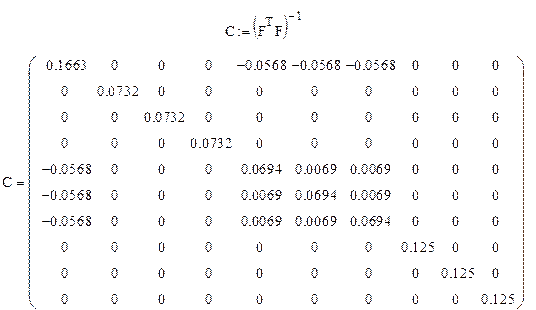
Из матрицы 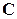 видно, что оценки
видно, что оценки 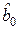 и все
и все 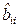 коррелированны между собой, о чем говорят соответствующие ненулевые элементы матрицы
коррелированны между собой, о чем говорят соответствующие ненулевые элементы матрицы 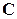 .
.
Найдем оценки коэффициентов 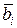
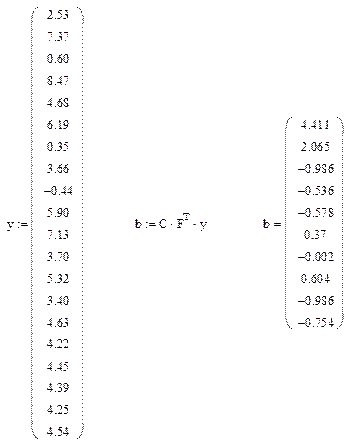
Для проверки статистической значимости коэффициентов найдем оценку дисперсии единичного наблюдения:
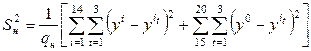
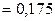 ,
,
где 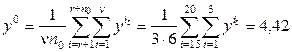 ;
;
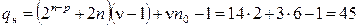 – число степеней свободы.
– число степеней свободы.
По соотношениям (3.2) найдем оценки дисперсий полученных коэффициентов регрессии:
– для  :
: 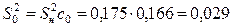 ;
;
– для 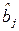 :
: 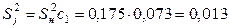 ,
, 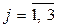 ;
;
– для 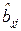 :
: 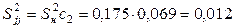 ,
, 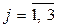 ;
;
– для 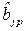 :
: 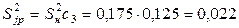 ,
, 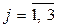 ,
, 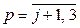 .
.
По критерию Стьюдента (3.3) определим статистическую значимость коэффициентов регрессии при 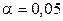 . Из табл. 3.4 видно, что статистически незначимым оказался коэффициент при квадратичном члене
. Из табл. 3.4 видно, что статистически незначимым оказался коэффициент при квадратичном члене 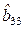 , который необходимо исключить из математической модели. Поскольку это приводит к изменению оценок коэффициентов
, который необходимо исключить из математической модели. Поскольку это приводит к изменению оценок коэффициентов 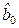 ,
, 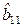 ,
, 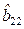 , то эти оценки и их дисперсии нужно рассчитать заново (исключив квадратный член
, то эти оценки и их дисперсии нужно рассчитать заново (исключив квадратный член 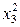 ):
):
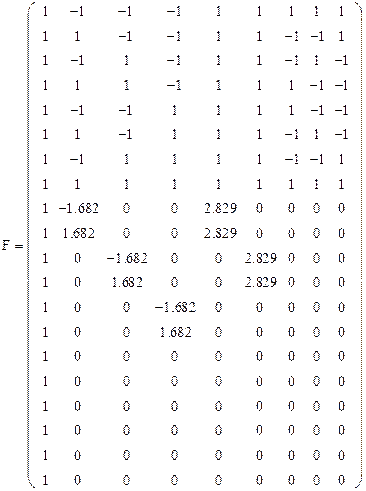
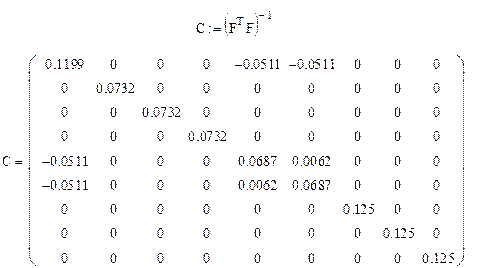
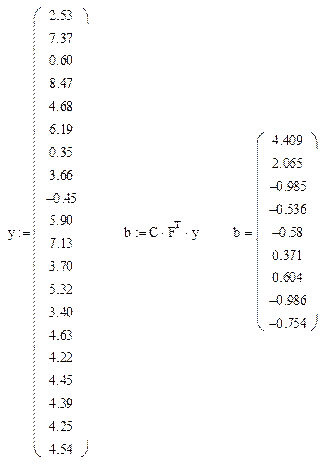
По критерию Стьюдента вновь определим статистическую значимость коэффициентов регрессии при 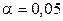 . На этот раз все коэффициенты оказались статистически значимыми (табл. 3.5).
. На этот раз все коэффициенты оказались статистически значимыми (табл. 3.5).
По критерию Фишера (1.5) проверим адекватность ММ при 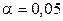 . При этом оценка дисперсии неадекватности
. При этом оценка дисперсии неадекватности 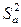 определяется выражением
определяется выражением
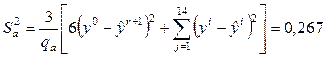 ,
,
где 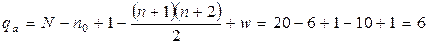 – число степеней свободы,
– число степеней свободы, 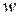 – число незначимых коэффициентов регрессии.
– число незначимых коэффициентов регрессии.
Так как 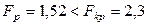 , то модель считаем адекватной.
, то модель считаем адекватной.
 2015-05-13
2015-05-13 495
495







