Для записи ММ в реальных физических величинах производят обратный переход от стандартизованного масштаба к натуральному. Это можно сделать, используя соотношение (2.1). После этого записывают окончательный вид модели.
2.7. Пример выполнения ортогонального центрального
композиционного эксперимента
Пусть при трех сериях опытов с помощью ортогонального центрального композиционного эксперимента требуется исследовать влияние производственных факторов
(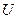 – опорное напряжение
– опорное напряжение 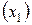 ,
, 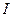 – ток потребления
– ток потребления 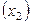 ,
, 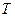 – конечная температура нагрева
– конечная температура нагрева 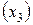 ) на качество производства магнитных дисков. Номинальные значения факторов:
) на качество производства магнитных дисков. Номинальные значения факторов: 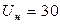 В,
В, 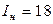 А,
А, 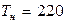
 .
.
Условия проведения опытов сведем в табл. 2.5 и проведем нормализацию масштабов факторов.
Таблица 2.5
Условия проведения опытов при ортогональном ЦКП эксперимента
| Характеристика плана | Натуральный масштаб | Нормиро-ванный
масштаб 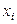
| ||
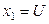 , В , В
| 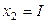 , А , А
| 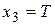 , , 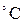
| ||
| Нулевой уровень | ||||
| Верхний уровень | +1 | |||
| Нижний уровень | –1 | |||
| Звездные точки | 33,645 | 20,43 | 244,3 | +1,215 |
| 26,355 | 15,57 | 195,7 | –1,215 |
Cоставим МП эксперимента, в соответствии с которой проведем рандомизированные опыты. Полученные результаты запишем в табл. 2.6, где 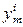 – численные значения исследуемого параметра,
– численные значения исследуемого параметра, 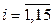 – номер точки в факторном пространстве,
– номер точки в факторном пространстве,
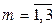 – номер параллельного опыта. В эту же таблицу будем записывать и другие получаемые результаты.
– номер параллельного опыта. В эту же таблицу будем записывать и другие получаемые результаты.
Проведем статистическую обработку полученных результатов. Для проверки по критерию Кохрена (2.2) воспроизводимости опытов при выбранном уровне значимости 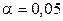 вычислим в каждой точке факторного пространства (в нашем случае их
вычислим в каждой точке факторного пространства (в нашем случае их 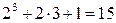 ) среднее значение
) среднее значение
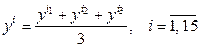
и оценку дисперсии исследуемого параметра
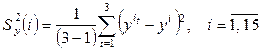 .
.
Рассчитаем оценки коэффициентов регрессионного уравнения. Для этого составим матрицу планирования 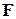 :
:
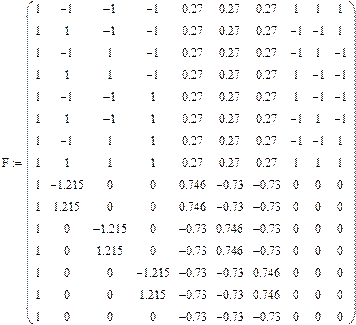
Найдем дисперсионную матрицу 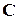 :
:
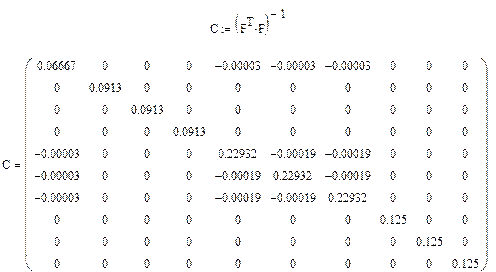
Заметим, что часть недиагональных элементов матрицы 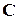 получилась отличной от нуля, что противоречит теории. Это противоречие объясняется неточностью выбора плеча
получилась отличной от нуля, что противоречит теории. Это противоречие объясняется неточностью выбора плеча 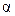 , которая привела к появлению очень незначительной коррелированности некоторых оценок регрессионных коэффициентов.
, которая привела к появлению очень незначительной коррелированности некоторых оценок регрессионных коэффициентов.
Составим вектор наблюдений и вычислим оценки коэффициентов
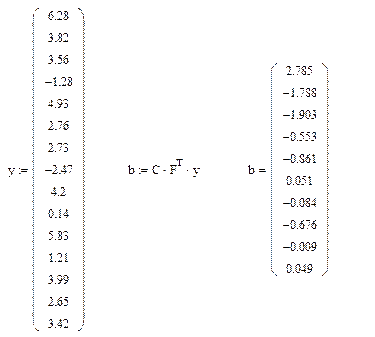
Найдем оценку дисперсии единичного наблюдения:
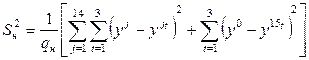
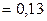 ,
,
где 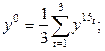
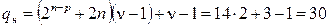 .
.
По соотношениям (2.3) вычислим оценки дисперсий коэффициентов регрессии:
– для 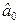 :
: 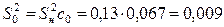 ;
;
– для 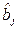 :
: 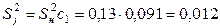 ,
, 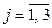 ;
;
– для 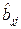 :
: 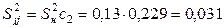 ,
, 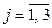 ;
;
– для 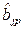 :
: 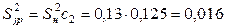 ,
, 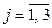 ,
, 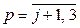 .
.
По критерию Стьюдента (2.4) определим статистическую значимость коэффициентов регрессии при 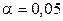 . Все полученные результаты внесем в табл. 2.6. Исключим из ММ незначимые коэффициенты регрессии. При этом, благодаря ортогональности плана, оценки остальных коэффициентов не изменятся.
. Все полученные результаты внесем в табл. 2.6. Исключим из ММ незначимые коэффициенты регрессии. При этом, благодаря ортогональности плана, оценки остальных коэффициентов не изменятся.
По критерию Фишера (1.5) проверим адекватность ММ при 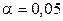 . Оценку дисперсии неадекватности вычислим по соотношению (2.6)
. Оценку дисперсии неадекватности вычислим по соотношению (2.6)
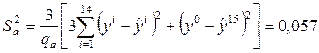 ,
,
где 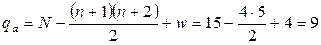 – число степеней свободы.
– число степеней свободы.
Найдем 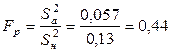 и
и 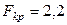 (используя таблицу F-распределения (прил. 3) и число степеней свободы числителя
(используя таблицу F-распределения (прил. 3) и число степеней свободы числителя 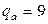 и знаменателя
и знаменателя 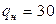 ).
).
Так как 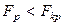 , то полученную модель считаем адекватной.
, то полученную модель считаем адекватной.
 2015-05-13
2015-05-13 582
582








