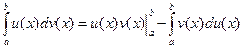 .
.
Задача 4.2.а. Найти площадь фигуры, ограниченной линиями 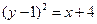 ,
, 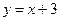 .
.
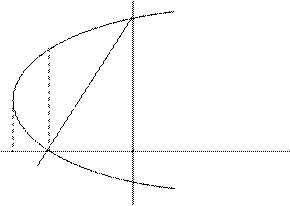
Решение. Заметим, что первое уравнение является уравнением параболы, ветви которой направлены вправо. Второе уравнение определяет прямую линию.
Найдем пересечения графиков функций и сделаем рисунок. Для этого решим систему
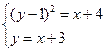 Û
Û 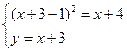
откуда 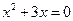 , что дает
, что дает 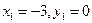 и
и 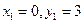 .
.
 3
3 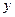
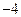
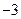 0
0 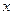
Из рисунка видно, что фигура состоит из двух частей. При 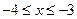 получаем сегмент параболы
получаем сегмент параболы 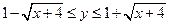 . При
. При 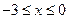 криволинейная трапеция заключена между прямой и параболой
криволинейная трапеция заключена между прямой и параболой 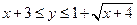 . Следовательно, площадь фигуры равна сумме двух следующих двух интегралов:
. Следовательно, площадь фигуры равна сумме двух следующих двух интегралов:
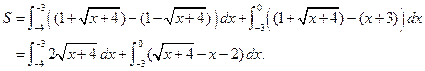 Для первого интеграла получаем:
Для первого интеграла получаем:
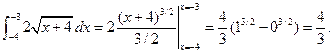
Для второго интеграла получаем:
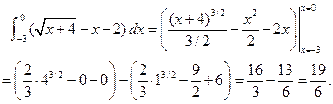
Таким образом, 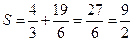 . Ответ:
. Ответ: 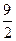 .
.
Задача 4.2.б. Найти площадь фигуры, ограниченной линиями 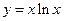 ,
, 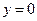 ,
, 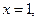
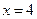 .
.
Решение. На отрезке 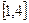 выполняется неравенство
выполняется неравенство 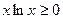 . Поэтому найдем площадь, используя формулу
. Поэтому найдем площадь, используя формулу 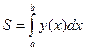 .
.
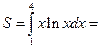
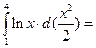
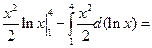
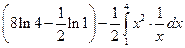
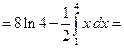
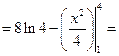
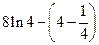 =
= 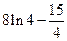 .
.
 2015-05-13
2015-05-13 318
318








