Определенный интеграл (Римана) позволяет распространить формулу площади прямоугольника на площадь более или менее произвольной плоской геометрической фигуры. В основе понятия определенного интеграла лежит так называемая интегральная сумма, определяемая следующим образом. Пусть задана функция 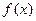 , определенная на отрезке
, определенная на отрезке 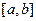 . Разобъем отрезок
. Разобъем отрезок 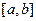 произвольным образом на
произвольным образом на 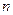 частей
частей 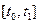 ,
, 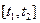 ¼,
¼, 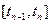 (
(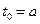 ,
, 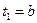 ). В частности, можно разбить
). В частности, можно разбить 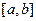 на
на 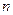 равных частей, тогда длина каждого отрезка разбиения будет равна
равных частей, тогда длина каждого отрезка разбиения будет равна 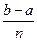 . В общем случае, пусть
. В общем случае, пусть
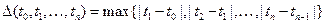 .
.
Возьмем, опять же произвольным образом, внутри каждого из отрезков 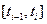 по точке
по точке 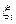 . Интегральной суммой функции
. Интегральной суммой функции 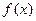 на
на 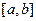 по разбиению
по разбиению 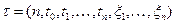 называется число
называется число
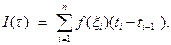
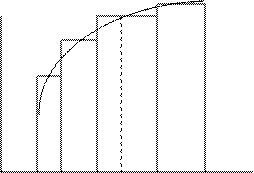
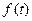
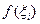
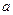
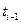
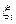
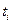
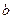
Если 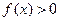 , то интегральная сумма есть площадь фигуры, состоящей из прямоугольников со сторонами
, то интегральная сумма есть площадь фигуры, состоящей из прямоугольников со сторонами 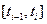 и
и 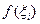 ,
, 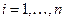 . Интуитивно ясно, что, чем меньше максимальная длина отрезков разбиения
. Интуитивно ясно, что, чем меньше максимальная длина отрезков разбиения 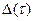 , тем точнее эта фигура из прямоугольников приближает криволинейную трапецию с основаниями
, тем точнее эта фигура из прямоугольников приближает криволинейную трапецию с основаниями 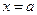 ,
, 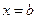 и “боковыми сторонами”
и “боковыми сторонами” 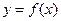 ,
, 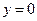 . Интеграл от функции
. Интеграл от функции 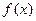 по отрезку
по отрезку 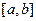 есть предел
есть предел 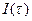 по всевозможным разбиениям
по всевозможным разбиениям 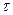 , когда
, когда 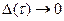 .
.
Предел понимается здесь в обычном смысле: число 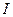 называется определенным интегралом от
называется определенным интегралом от 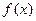 по
по 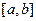 (обозначается как
(обозначается как 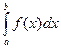 ), если для произвольного
), если для произвольного 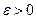 найдется такое
найдется такое 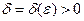 , что, как только разбиение
, что, как только разбиение 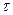 отрезка
отрезка 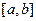 удовлетворяет условию
удовлетворяет условию 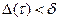 , интегральная сумма
, интегральная сумма 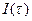 , отвечающая этому разбиению, будет отличаться от
, отвечающая этому разбиению, будет отличаться от 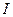 не больше, чем на
не больше, чем на 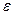 :
: 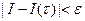 .
.
 2015-05-13
2015-05-13 315
315








