Теоретические основы

Нейрон сигмоидального типа (рис. 5) имеет непрерывную функцию активации и может быть выражена в виде сигмоидальной униполярной или биполярной функции. Униполярная функция, как правило, представляется формулой:

,

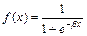тогда как биполярная функция задается в виде

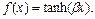
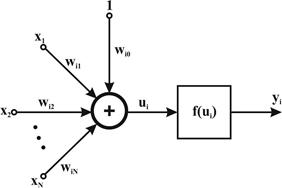
Рис. 5 Модель сигмоидального нейрона

В этих формулах параметр 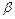подбирается пользователем. Его значение влияет на форму функции активации. На рис. 6 представлены графики сигмоидальной функции от переменной х для различных значений 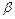, причем на рис. 6а показана униполярная, а на рис. 6б - биполярная функция. Графики обеих функций сильно зависят от значения 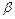. При малых величинах 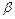график функции достаточно пологий, но по мере роста значения 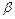крутизна графика увеличивается. При 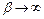сигмоидальная функция превращается в функцию ступенчатого типа, идентичную функции активации персептрона. На практике чаще всего для упрощения используется значение 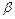= 1.

Важным свойством сигмоидальной функции является ее дифференцируемость. Для униполярной функции имеем

,

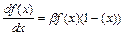тогда как для биполярной функции

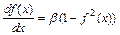
И в первом, и во втором случае график изменения производной относительно переменной х имеет колоколообразную форму, а его максимум соответствует значению х=0 (рис. 7).

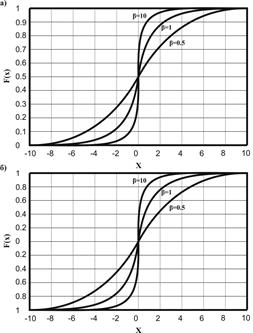
Рис 6. График сигмоидальной функции:

а) униполярной; б) биполярной при различных значениях коэффициента .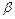

Сигмоидальный нейрон, как правило, обучается с учителем по принципу минимизации целевой функции, которая для единичного обучающего кортежа <x,d> i-го нейрона определяется в виде.

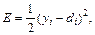(1)

Где

.

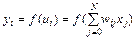Функция 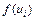является сигмоидальной, х - это входной вектор, х = [х0, x1,..., хN]T со значением x0=1 при наличии поляризации и x0=0 при ее отсутствии, а di - соответствующее ему ожидаемое значение на выходе i-гo нейрона.

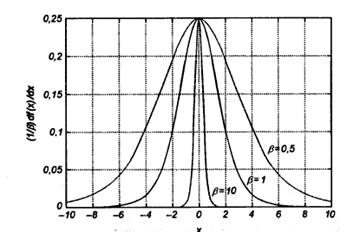
Рис 7. График производной от сигмоидальной функции при различных значениях коэффициента .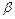

Применение непрерывной функции активации позволяет использовать при обучении градиентные методы. Проще всего реализовать метод наискорейшего спуска, в соответствии с которым уточнение вектора весов 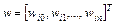проводится в направлении отрицательного градиента целевой функции. Если эта функция определена выражением (1), j-я составляющая градиента имеет вид:

,

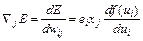где е_i = (у_i - d_j) означает разницу между фактическим и ожидаемым значением выходного сигнала нейрона. Если ввести обозначение 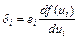, то можно получить выражение, определяющее j-ю составляющую градиента в виде

.

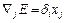Значения весовых коэффициентов также могут уточняться дискретным способом:

,

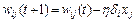где 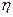- это коэффициент обучения, значение которого, как правило, выбирают эмпирически из интервала (0,1).

Задание к лабораторной работе:

На основе теоретических основ создать алгоритм подбора весовых коэффициентов методом наискорейшего спуска и дискретным способом. Реализовать данный алгоритм программно. Программа должна содержать ввод: динамической матрицы входных сигналов; желаемого значения, допустимый процент погрешности обучения, возможность выбора метода обучения, а для дискретного метода возможность установки коэффициента обучения; вывод: матрица весовых коэффициентов, значение выходной функции, количество итераций обучения.

На основе программы построить зависимость между числом входных сигналов (от 3 до 10) и количеством итерации необходимых для обучения нейрона. Сравнить полученные зависимости для дискретного и градиентного метода обучения.

Оформить отчет, который должен содержать блок схему программы и полученные зависимости.

Контрольные вопросы

1. Какие функции активации применяются в сигмоидальном нейроне?

2. Как производиться обучение сигмоидального нейрона?

3. На что влияет коэффициент обучения?

4. Для чего в функциях активации сигмоидального нейрона применяется параметр .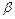

Лабораторная работа №4
Инстар и оутстар Гроссберга

Цель работы: Изучить принцип обучения нейрона- инстар и оутстар Гроссберга.

Теоретические основы

Нейроны типа инстар и оутстар - это взаимодополняющие элементы. Инстар адаптирует веса сигналов, поступающих на сумматор нейрона, к своим вход­ным сигналам, а оутстар согласовывает веса выходящих из нейрона связей с узлами, в которых формируются значения выходных сигналов. Нейрон типа инстар был определен С. Гроссбергом. На рис. 8 представлена структурная схема инстара.

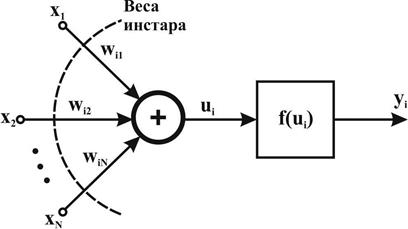
Рис. 8. Структурная схема инстара

Сигналы x_j, подаваемые с весовыми коэффициентами w_ij на вход i-гo инстара, суммируются в соответствии с выражением

.

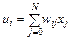В соответствии с функцией активации на выходе нейрона вырабатывается выходной сигнал 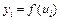.Часто в инстаре применяется линейная форма функции активации, и тогда 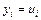. Обучение инстара (подбор весов w_ij) производится по правилу Гроссберга, в соответствии с которым

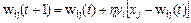. (1)

где 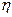- это коэффициент обучения, значение которого, как правило, выби­рается из интервала (0,1). Входные данные, представляемые в виде вектора х, выражены чаще всего в нормализованной форме, в которой ||x|| = 1. Норма­лизация компонентов вектора х выполняется по формуле

.

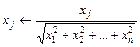Результаты обучения по методу Гроссберга в значительной степени зависят от коэффициента обучения 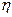. При выборе 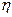= 1 веса w_ij становятся равными значениям x_j уже после первой итерации. Ввод очередного входного вектора x вызовет адаптацию весов к новому вектору и абсолютное "забывание" предыдущих значений. Выбор 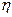< 1 приводит к тому, что в результате обучения весовые коэффициенты w_ij принимают усредненные значения обучающих векторов х.

Допустим, что i-й инстар был обучен на некотором нормали­зованном относительно своих компонентов входном векторе x₁. В этом случае на векторе весов инстара выполняется отношение: 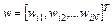. В режиме классификации при вводе очередного входного вектора x₂ инстар вырабатывает сигнал u_i вида

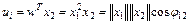
Вследствие нормализации амплитуд входных векторов получаем:

.

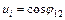При выполнении условия x₂= x₁ реакция инстара будет равна u_i= 1. В слу­чае, когда входные векторы отличаются друг от друга, реакция инстара будет пропорциональна косинусу угла между этими векторами. Для ортогональных векторов u_i= 0.

В итоге натренированный инстар функционирует как векторный класси­фикатор, сопоставляющий очередной поданный на его вход вектор с вектором, сформированным в процессе обучения. В случае максимального совпа­дения этих векторов реакция инстара будет максимальной (наиболее близкой к единице). Если инстар обучался на группе достаточно похожих векторов с коэффициентом обучения 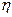< 1, то его весовые коэффициенты примут значения, усредненные по этим векторам, и в режиме классифи­кации он будет лучше всего реагировать на входные векторы, параметры которых наиболее близки к средним значениям векторов, входивших в обучающую группу.

Необходимо подчеркнуть, что инстар может обучаться как с учителем, так и без него. Во втором случае в правиле Гроссберга в качестве значения у_i, принимается фактическое значение выходного сигнала инстара. При обучении с учителем значение у_i заменяется ожидаемым значением d_i, т.е. у_i = d_i.

Для примера рассмотрим обучение четырехвходового инстара с одноступенчатой функцией активации. Инстар тренируется с учителем, а обучающие векторы х и значения d имеют вид:

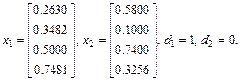
Значение весового коэффициента поляризации принято равным - 0, 95. Это означает, что выходной сигнал нейрона будет равен 1 при u_i = 0,95, т.е. при значении u_i достаточно близком к единице. При нулевых начальных значениях весов и коэффициенте обучения 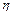= 0,4 при обучении с учителем стабилизация значений весов была достигнута уже после десяти циклов обучения. Численные результаты обучения имеют вид

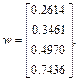
достаточно близкий к реализации первого входного вектора x₁. При выборе коэффициента обучения 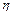= 0,75 нейрон оказался натренированным уже после четырех циклов обучения. Второй вектор x₂ в процессе обучения с учителем не оказывал никакого влияния на результаты обучения вследствие того, что d₂ = 0.

В процессе функционирования при подаче на вход вектора x₁ выраба­тывается значение u₁ = 0,9940, при котором нейрон формирует выходной сигнал, равный 1. При подаче на вход вектора x₂ вырабатывается значение u₂= 0,7961< 0,95, при котором нейрон формирует нулевой выходной сигнал.

Нейрон типа оутстар Гроссберга представляет собой комплементарное дополнение инстара. Если инстар обучается с целью распознавать вектор, подаваемый на его вход, то оутстар должен генерировать вектор, необходимый связанным с ним нейронам. Структурная схема оутстара представлена на рис. 9. i-й нейрон-источник высылает свой выходной сигнал у_i, взаимодействующим с ним нейронам, выходные сигналы которых обозначены y_j(j = 1, 2,..., М). Оутстар, как правило, является линейным нейроном. Обучение состоит в таком подборе его весов w_ij, чтобы выходные сигналы оутстара были равны ожидаемым значениям y_j взаимодействующих с ним нейронов. Обучение оутстара согласно правилу Гроссберга проводится в соответствии с выражением

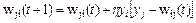, (2)

в котором 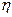- это коэффициент обучения, а у_i - выходной сигнал i-го нейрона, выступающего в роли источника. Зависимость (2) для оутстара аналогична выражению (1), по которому обучается инстар. В режиме распознавания в момент активизации нейрона-источника оутстар будет генерировать сигналы, соответствующие ожидаемым значениям y_j.

Основу обучения персептрона, сигмоидального нейрона и адалайна составляет пара обучающих векторов (х, d). Они могут обучаться только с учителем. При обучении инстара и оутстара весовые коэффициенты подстраиваются под входные или выходные векторы. Обучение может проводиться как с учителем, так и без него.

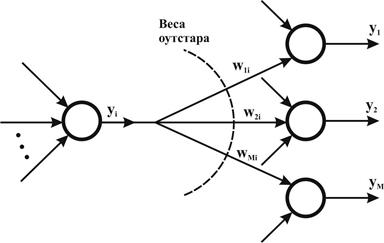
Рис. 9. Структурная схема оутстара

Задание к лабораторной работе:

На основе теоретических основ создать алгоритм подбора весовых коэффициентов инстара методом описанным формулой 1. Реализовать данный алгоритм программно. Программа должна содержать ввод: двух динамических матриц входных сигналов; желаемых значений, допустимый процент погрешности обучения, возможность установки коэффициента обучения; вывод: матрица весовых коэффициентов, значения выходных функции, количество итераций обучения.

Оформить отчет, который должен содержать блок схему программы.

Контрольные вопросы

1. Какие функции активации используются в нейронах оутстар и инстар Гроссберга.

2. Как производиться обучение с учителем в нейронах оутстар и инстар Гроссберга.

3. Как производиться обучение без учителя в нейронах оутстар и инстар Гроссберга.

4. Как производиться нормализация входного вектора.

Лабораторная работа №5
Модель нейрона Хебба

Цель работы: Изучить принцип обучения нейрона Хебба.

Теоретические основы

Д. Хебб в процессе исследования нервных клеток заметил, что связь между двумя клетками усиливается, если обе клетки пробуждаются (становятся активными) в один и тот же момент времени. Если j-я клетка с выходным сигналом y_j связана с i-й клеткой, имеющей выходной сигнал y_i, связью с весом w_ij, то на силу связи этих клеток влияют значения выходных сигналов y_j и y_i

Д. Хебб предложил формальное правило, в котором отразились результаты его наблюдений. В соответствии с правилом Хебба, вес w_ij нейрона изменяется пропорционально произведению его входного и выходного сигналов

,

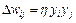(1)

где 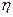- это коэффициент обучения, значение которого выбирается в интервале (0,1). Правило Хебба может применяться для нейронных сетей различных типов с разнообразными функциями активации моделей отдельных нейронов.

Структурная схема нейрона Хебба, представленная на рис. 10, соответствует стандартной форме модели нейрона. Связь с весом w_iy, способ подбора значения которого задается отношением (1), соединяет входной сигнал y_j с сумматором i-го нейрона, вырабатывающего выходной сигнал у_i. Обучение нейрона по правилу Хебба может проводиться как с учителем, так и без него. Во втором случае в правиле Хебба используется фактическое значение у_i, выходного сигнала нейрона. При обучении с учителем вместо значения выходного сигнала у_i, используется ожидаемая от этого нейрона реакция d_i. В этом случае правило Хебба записывается в виде

.

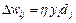Правило Хебба характеризуется тем, что в результате его применения веса могут принимать произвольно большие значения, поскольку в каждом цикле обучения происходит суммирование текущего значения веса и его приращения :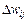

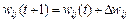
Один из способов стабилизации процесса обучения по правилу Хебба состоит в учете для уточнения веса последнего значения 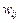, уменьшенного на коэффициент забывания 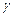. При этом правило Хебба представляется в виде

.

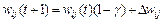Значение коэффициента забывания 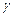выбирается, как правило, из интервала (0,1) и чаще всего составляет некоторый процент от коэффициента обучения 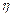. Применение больших значений 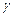приводит к тому, что нейрон забывает значительную часть того, чему он обучился в прошлом. Рекомендуемые значения коэффициента забывания - 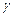< 0,1, при которых нейрон сохраняет большую часть информации, накопленной в процессе обучения, и получает возможность стабилизировать значения весов на определенном уровне.

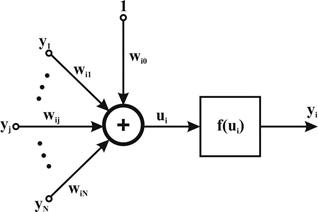
Рис. 10. Структурная схема нейрона Хебба

В качестве примера рассмотрим обучение без учителя с забыванием сети, состоящей из четырех нейронов с одноступенчатой нелинейностью, причем на входы каждого нейрона подаются все четыре компонента вектора (рис. 11). Примем, что веса поляризации w_i0 для i = 1, 2, 3, 4 постоянны и равны -0,5.

Обучающие выборки х представлены в следующем виде:

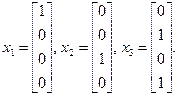
Начальные значения весовых коэффициентов w_ij заданы единичной матрицей w, в которой каждый i -й столбец соответствует весам j-ro нейрона:

.

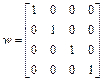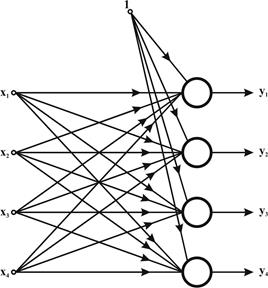
Рис. 11. Структура сети Хебба

После нескольких циклов обучения при 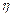= 0,1 и 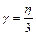матрица весов приняла вид:

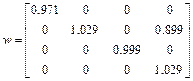
В результате обучения связи между четвертым нейроном и вторым входом, а также между вторым нейроном и четвертым входом были усилены. После проведенного тренинга оба нейрона (второй и четвертый) одинаково реагируют на единичный сигнал, поступающий как на второй, так и на четвертый вход. Веса первого и третьего нейронов подверглись минимальным изменениям, соответствующим принятым коэффициентам обучения 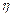и забывания 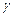. Сеть самостоятельно (обучение проводилось без учителя) обрела способность распознавать определенные зависимости между вторым входом и четвертым нейроном, а также между четвертым входом и вторым нейроном. По этой причине обучение по Хеббу считается обучением ассоциативного типа.

Задание к лабораторной работе:

На основе теоретических основ создать алгоритм подбора весовых коэффициентов нейрона Хебба. Реализовать данный алгоритм программно. Программа должна содержать ввод: трех динамических матриц входных сигналов; вывод: матрица весовых коэффициентов и значения выходных функции после определенного количества итераций обучения. Проанализировать изменения весов взависимости от количества обучающих итераций.

Оформить отчет, который должен содержать блок схему программы.

Контрольные вопросы

1. Что собой представляет правило Хебба?

2. Как производиться обучение нейрона Хебба?

3. На что влияет коэффициент забывания .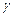

Приложение 1

Значение коэффициентов	х – базовое множество, на котором определяется ФП; а и с - основание треугольника; b – его вершина.	х – базовое множество, на котором определяется ФП; а и d – нижнее основание трапеции; b и с –верхнее основание трапеции.
Графическое представление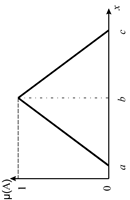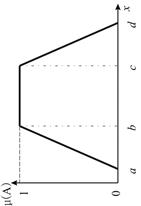
Аналитическая запись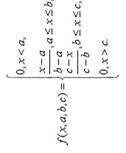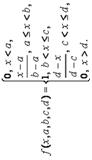
Название ФП	Треугольная	Трапеципе-видная
№ п/п

Продолжение приложение 1

Значение коэффициентов	х – базовое множество, на котором определяется ФП; с – определяет расположение центра ФП; 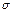– оказывает влияние на форму кривой.	с – определяет расположение центра ФП; а и b – оказывают влияние на форму кривой.
Графическое представление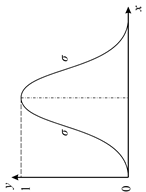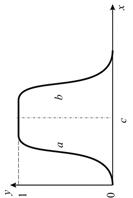
Аналитическая запись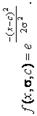
Название ФП	Симметричная функция Гаусса	Функция «обобщенный колокол»
№ п/п

Продолжение приложение 1

Значение коэффициентов	с – определяет расположение центра ФП; а – оказывает влияние на форму кривой В зависимости от знака параметра a рассматриваемая ФП будет открыта или справа или слева, что позволяет применять ее при описании таких нечетких понятий, как «очень большой», «крайне отрицательно» и др.
Графическое представление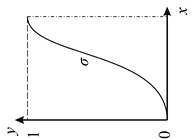
Аналитическая запись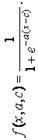
Название ФП	Сигмойдная
№ п/п

Список литературы

1. Зубков Е.В., Макушин А.А., Илюхин А.Н. Применение нечеткой логики для моделирования режимов испытания двигателей внутреннего сгорания //Сборка в машиностроении, приборостроении. – 2009 - № 8. – С. 39-44.

2. Илюхин А.Н. Применение нечеткой логики в автоматизированной системе испытаний ДВС // Проектирование и исследование технических систем: Межвузовский научный сборник. Вып.12. /Под ред. доктора техн. наук проф. В.Г. Шибакова – Набережные Челны: Изд-во Камской государственной инженерно-экономической академии, 2008. – С. 65-73.

3. Круглов В.В., Дли М.И., Голунов Р.Ю. Нечеткая логика и искусственные нейронные сети. – М.: -Физматлит, 2001.

4. Осовский С. Нейронные сети для обработки информации / Пер. с польского. – М.: Финансы и статистика, 2002. – 344 с., ил.

5. Ярушкина Н.Г Основы нечетких и гибридных систем: учеб. пособие. - М: Финансы и статистика, 2004. – 320 с.: ил.