1. Переменная 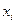 называется базисной, если она с коэффициентом 1 входит только в одно уравнение системы ограничений и не входит в функцию
называется базисной, если она с коэффициентом 1 входит только в одно уравнение системы ограничений и не входит в функцию 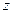 .
.
2. Если в системе ограничений имеется ровно 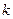 базисных переменных, то скажем, что получен опорный план. При этом небазисные переменные называются свободными. Опорный план - это допустимый набор
базисных переменных, то скажем, что получен опорный план. При этом небазисные переменные называются свободными. Опорный план - это допустимый набор 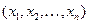 , в котором базисные переменные равны элементам свободного столбца
, в котором базисные переменные равны элементам свободного столбца 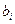 , а свободные переменные равны нулю.
, а свободные переменные равны нулю.
Критерий оптимальности опорного плана: все коэффициенты при свободных переменных в функции 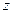 отрицательны или равны 0.
отрицательны или равны 0.
Улучшение опорного плана.
Пусть опорный план не оптимален, то есть
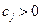
для какой-либо свободной переменной 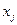 .
.
Утверждение. Можно увеличить значение функции 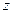 , если перейти к новому опорному плану, который получается при помощи полного жорданова исключения с разрешающим столбцом
, если перейти к новому опорному плану, который получается при помощи полного жорданова исключения с разрешающим столбцом 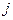 и разрешающей строкой, которая выбирается по следующему правилу.
и разрешающей строкой, которая выбирается по следующему правилу.
Составим отношения
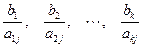
для всех 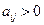 . Тогда разрешающая строка – та, в которой достигается минимум из этих отношений.
. Тогда разрешающая строка – та, в которой достигается минимум из этих отношений.
Если все отношения отрицательны, то максимум функции 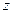 равен
равен 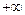 .
.
Получение опорного плана – двухэтапный метод.
Пусть ровно в одном уравнении системы не хватает базисной переменной. Например, в уравнении №1. Введем дополнительную переменную 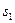 в это уравнение:
в это уравнение:
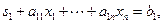
и рассмотрим вспомогательную задачу
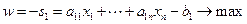
Для этой задачи имеется опорный план. Оптимальный план для вспомогательной задачи является опорным планом для исходной задачи. Если у вспомогательной задачи максимум функции 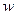 равен
равен 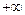 , то у исходной задачи - нет решений. Если в нескольких уравнениях системы не хватает базисных переменных, то в каждое из этих уравнений надо добавить свою вспомогательную переменную
, то у исходной задачи - нет решений. Если в нескольких уравнениях системы не хватает базисных переменных, то в каждое из этих уравнений надо добавить свою вспомогательную переменную 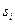 , и решить задачу
, и решить задачу 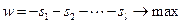 .
.
 2015-05-13
2015-05-13 564
564








