Рассмотрим производство, состоящее из 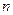 взаимосвязанных подразделений (отраслей), которые в процессе производства продукции затрачивают некоторое количество продукции, производимой в других подразделениях. Таким образом, валовой продукт всех подразделений складывается из двух частей – конечного продукта и внутрипроизводственного потребления. Задачей межотраслевого баланса является определение соотношений между конечным и валовым продуктом, нахождение чистого продукта отрасли, а также определение себестоимости производства продукции.
взаимосвязанных подразделений (отраслей), которые в процессе производства продукции затрачивают некоторое количество продукции, производимой в других подразделениях. Таким образом, валовой продукт всех подразделений складывается из двух частей – конечного продукта и внутрипроизводственного потребления. Задачей межотраслевого баланса является определение соотношений между конечным и валовым продуктом, нахождение чистого продукта отрасли, а также определение себестоимости производства продукции.
Для простоты предполагается, что каждое подразделение производит только один вид продукции. Будем считать, что нам известно то количество продукции, которое потребляется в процессе производства одной единицы продукции каждой отрасли. Соответствующие коэффициенты называются коэффициентами прямых производственных затрат. Пусть 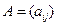 –
– 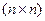 -матрица коэффициентов прямых производственных затрат, где
-матрица коэффициентов прямых производственных затрат, где 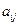 есть количество продукции
есть количество продукции 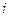 –й отрасли, потребляемое в процессе производства одной единицы продукции
–й отрасли, потребляемое в процессе производства одной единицы продукции 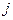 –й отрасли. Обозначим через
–й отрасли. Обозначим через 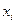 валовой продукт
валовой продукт 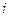 –й отрасли, а через
–й отрасли, а через 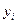 – ее конечный продукт. Представление
– ее конечный продукт. Представление
валовой продукт = конечный продукт + внутрипроизводственное потребление
запишется в виде уравнения
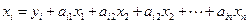 ,
, 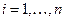 ,
,
или, в матричных обозначениях, в виде
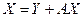 .
.
Это уравнение называется уравнением межотраслевого баланса. Теперь количество продукции 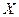 , которое необходимо произвести, чтобы обеспечить заданное количество конечного продукта
, которое необходимо произвести, чтобы обеспечить заданное количество конечного продукта 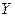 , получается как решение данного матричного уравнения
, получается как решение данного матричного уравнения
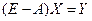 Û
Û 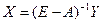 .
.
Матрица называется матрицей коэффициентов полных производственных затрат. Разница между полными производственными затратами и прямыми производственными затратами называется косвенными затратами. Таким образом, матрица
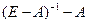
есть матрица коэффициентов косвенных производственных затрат. Чистый продукт отрасли есть ее валовой продукт минус то количество продукции, которое было затрачено на производство этого валового продукта во всех отраслях:
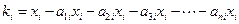 ,
, 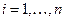 .
.
Нетрудно видеть, что суммарный конечный продукт суммарный чистый продукт отраслей равны:
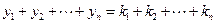 .
.
Рассмотрим теперь механизм образования себестоимости продукции. Предположим, что для производства одной единицы (валовой) продукции 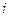 –й отрасли необходимо затратить
–й отрасли необходимо затратить 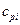 единиц
единиц 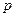 –го сырья,
–го сырья, 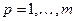 . Сырье понимается в широком смысле слова: закупаемые материалы, электроэнергия, производственные фонды, труд и т.д. Обозначим
. Сырье понимается в широком смысле слова: закупаемые материалы, электроэнергия, производственные фонды, труд и т.д. Обозначим 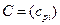
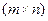 -матрицу удельных коэффициентов прямых затрат сырья. Тогда полные затраты
-матрицу удельных коэффициентов прямых затрат сырья. Тогда полные затраты 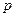 –го вида сырья, необходимые для производства валового продукта
–го вида сырья, необходимые для производства валового продукта 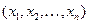 равны
равны
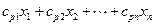 .
.
Следовательно полные затраты всех видов сырья, необходимого на выполнение производственного задания, есть вектор
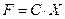 .
.
Определим затраты сырья в пересчете на 1 единицу конечной продукции 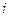 –й отрасли. С учетом соотношения
–й отрасли. С учетом соотношения 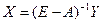 получаем
получаем
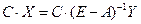 .
.
Таким образом, матрица 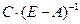 есть матрица коэффициентов полных затрат сырья.
есть матрица коэффициентов полных затрат сырья.
Если известен вектор цен на одну единицу сырья каждого вида,
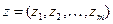 ,
,
то полные затраты на производство конечного продукта 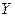 равны
равны
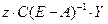 ,
,
а себестоимость производства одной единицы продукции 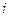 -й отрасли равна
-й отрасли равна
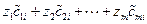 ,
,
где 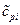 - элемент матрицы
- элемент матрицы 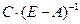 , стоящий в
, стоящий в 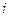 -й строке,
-й строке, 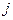 -м столбце.
-м столбце.
Задача 6.1. Химическое предприятие состоит из двух основных и одного вспомогательного цехов, каждый из которых выпускает один вид продукции. Прямые затраты aij продукции i -го цеха на производство 1 единицы продукции j -го цеха, а также величины конечного продукта 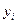 , представлены таблицей.
, представлены таблицей.
| Цеха | Коэффициенты прямых затрат aij | Конечный продукт yi | ||
| I | II | III | ||
| I | 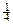 | |||
| II | 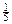 | 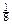 | 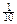 | |
| III | 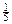 | 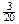 |
Определить: 1) коэффициенты полных затрат; 2) валовой выпуск для каждого цеха; 3) производственную программу цехов (распределение валового продукта на конечный продукт и внутрипроизводственное потребление раздельно по цехам); 4) коэффициенты косвенных затрат.
Решение. Выпишем матрицу прямых производственных затрат.
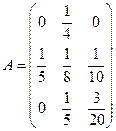
Определим матрицу полных производственных затрат.
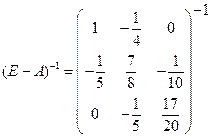
Получаем:
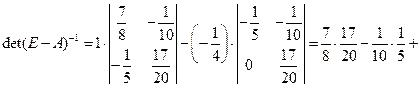
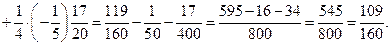
Для вычисления матрицы 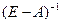 используем формулу
используем формулу 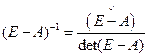 , где
, где 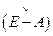 - присоединенная матрица, то есть матрица, состоящая из алгебраических дополнений элементов матрицы
- присоединенная матрица, то есть матрица, состоящая из алгебраических дополнений элементов матрицы 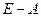 .
.
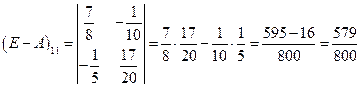 ;
; 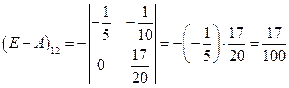 ;
; 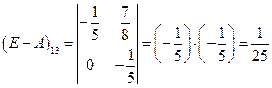 ;
;
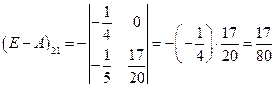 ;
; 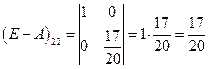 ;
; 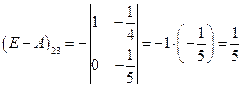 ;
; 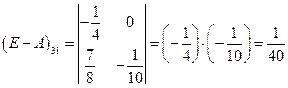 ;
; 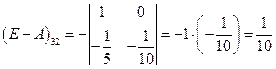 ;
; 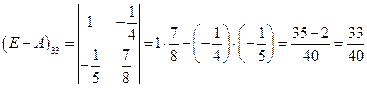 .
.
Записав алгебраические дополнения элементов строк в соответствующие столбцы, и поделив на определитель матрицы 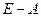 , получим
, получим
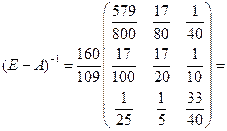
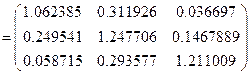
Определим валовой продукт каждого цеха. Поскольку конечный продукт есть 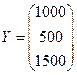 , валовой продукт находим по формуле
, валовой продукт находим по формуле
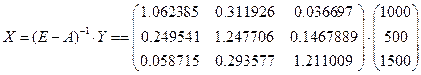
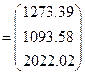 .
.
Рассмотрим распределение валового продукта цехов на конечный продукт и продукт, потребляемый в процессе производства в каждом из цехов. Для первого цеха из уравнения баланса получаем:
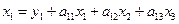 Û
Û 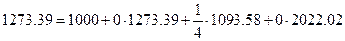
Следовательно, произведенные 1273.39 единиц продукции 1-го цеха распределяются следующим образом: 1000 единиц составляют конечный продукт, и 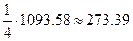 единицы продукции потребляются во втором цехе. Внутрипроизводственное потребление продукта 1-го цеха в самом 1-м цеху и в цехе №3 равны 0.
единицы продукции потребляются во втором цехе. Внутрипроизводственное потребление продукта 1-го цеха в самом 1-м цеху и в цехе №3 равны 0.
Для второго цеха получаем
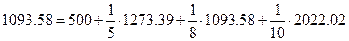
Таким образом, 1093.58 единицы продукции второго цеха дают 500 единиц конечного продукта, 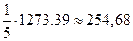 единицы потребляются в цехе №1,
единицы потребляются в цехе №1, 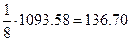 единицы потребляются в процессе производства в цехе №2, и, наконец,
единицы потребляются в процессе производства в цехе №2, и, наконец, 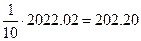 единицы потребляются в цехе №3. Суммарное внутрипроизводственное потребление продукта 2-цеха составляет 254.68+136.0+202,2=593,58 единицы.
единицы потребляются в цехе №3. Суммарное внутрипроизводственное потребление продукта 2-цеха составляет 254.68+136.0+202,2=593,58 единицы.
Составим баланс для третьего цеха. Получаем:
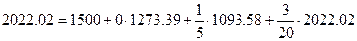 .
.
Имеем 1500 единиц конечного продукта, 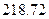 продукта третьего цеха потребляется во втором цеху,
продукта третьего цеха потребляется во втором цеху, 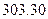 единиц потребляется в самом цехе №3, и 0 единиц потребляется в первом цеху. Суммарное внутрипроизводственное потребление составляет 218.72+303.30=522.02 единицы продукции третьего цеха.
единиц потребляется в самом цехе №3, и 0 единиц потребляется в первом цеху. Суммарное внутрипроизводственное потребление составляет 218.72+303.30=522.02 единицы продукции третьего цеха.
Матрица коэффициентов косвенных затрат имеет вид
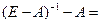
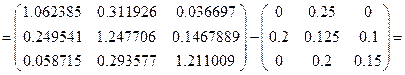
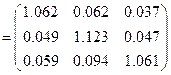 .
.
Задача полностью решена.
 2015-05-13
2015-05-13 1447
1447








