Предметом изучения математической статистики является определение законов распределения случайных величин и их параметров, если известны результаты измерений этих величин в серии реальных экспериментов.
Опишем типичную ситуацию статистического анализа. Мы изучаем некоторую случайную величину. Ее закон распределения (то есть, то, какие значения может принимать эта случайная величина, и с какой вероятностью это происходит) нам неизвестен. В математической статистике закон распределения случайной величины называется генеральной совокупностью. Мы проводим серию из 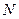 реальных физических опытов, в которых измеряем данную случайную величину. Результаты измерений
реальных физических опытов, в которых измеряем данную случайную величину. Результаты измерений 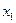 ,
, 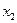 , ¼,
, ¼, 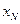 называются выборкой объема
называются выборкой объема 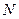 . Вопрос, как по данной выборке определить 1) математическое ожидание генеральной совокупности; 2) ее дисперсию; 3) к какому типу распределения относится данная генеральная совокупность и т.д. Разумеется, однозначно ответить на эти вопросы не возможно, поскольку информация о генеральной совокупности, заключенная в полученной выборке, не полна. Однако можно дать оценку тому или иному параметру генеральной совокупности, и, по возможности, оценить сверху вероятность ошибочного прогноза.
. Вопрос, как по данной выборке определить 1) математическое ожидание генеральной совокупности; 2) ее дисперсию; 3) к какому типу распределения относится данная генеральная совокупность и т.д. Разумеется, однозначно ответить на эти вопросы не возможно, поскольку информация о генеральной совокупности, заключенная в полученной выборке, не полна. Однако можно дать оценку тому или иному параметру генеральной совокупности, и, по возможности, оценить сверху вероятность ошибочного прогноза.
Статистикой для некоторого параметра 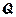 генеральной совокупности (например, для математического ожидания или дисперсии) называется случайная величина
генеральной совокупности (например, для математического ожидания или дисперсии) называется случайная величина
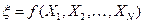 ,
,
которая зависит от 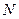 независимых одинаково распределенных случайных величин
независимых одинаково распределенных случайных величин 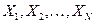 с тем же законом распределения, что и у генеральной совокупности, которая обладает хотя бы одним из следующих двух свойств:
с тем же законом распределения, что и у генеральной совокупности, которая обладает хотя бы одним из следующих двух свойств:
1) 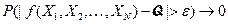 при
при 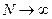 и любом положительном
и любом положительном 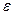 . Иными словами, вероятность уклонения
. Иными словами, вероятность уклонения 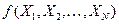 от
от 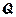 тем меньше, чем больше
тем меньше, чем больше 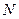 . Это свойство называется состоятельностью оценки.
. Это свойство называется состоятельностью оценки.
2) 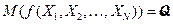 (несмещенность).
(несмещенность).
Отметим, что функция 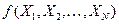 не должна зависеть от генеральной совокупности и должна обладать свойствами состоятельности или несмещенности сразу для всех возможных законов распределения.
не должна зависеть от генеральной совокупности и должна обладать свойствами состоятельности или несмещенности сразу для всех возможных законов распределения.
Если такая статистика найдена, то ее реализацию по данным нашей выборки, то есть число 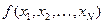 можно принять за статистическую (точечную) оценку параметра
можно принять за статистическую (точечную) оценку параметра 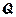 . Интервальной оценкой параметра
. Интервальной оценкой параметра 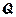 с доверительной вероятностью
с доверительной вероятностью 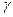 называется такой интервал
называется такой интервал 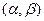 , где
, где 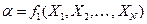 и
и 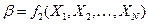 являются функциями от
являются функциями от 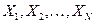 , что
, что
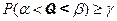 .
.
На базе центральной предельной теоремы Ляпунова можно указать статистики для точечных и интервальных оценок математического ожидания и дисперсии генеральной совокупности, а также при заданном уровне значимости проверить выполнение гипотезы о том, что генеральная совокупность распределена по нормальному закону. Приведем соответствующие формулы и алгоритм, основанный на так называемом критерии Пирсона.
Прежде всего, если объем выборки 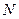 достаточно велик, производится так называемое группирование экспериментальных данных. Для этого числа
достаточно велик, производится так называемое группирование экспериментальных данных. Для этого числа 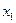 ,
, 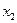 , ¼,
, ¼, 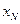 сначала записываются в порядке возрастания, затем определяется наименьший отрезок
сначала записываются в порядке возрастания, затем определяется наименьший отрезок 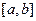 , содержащие все экспериментальные данные, после чего этот отрезок разбивается на
, содержащие все экспериментальные данные, после чего этот отрезок разбивается на 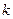 равных частей. Обозначим
равных частей. Обозначим 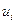 середину
середину 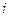 -го отрезка разбиения,
-го отрезка разбиения, 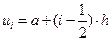 ,
, 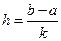 ,
, 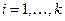 . Пусть
. Пусть 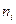 обозначает число точек выборки
обозначает число точек выборки 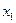 ,
, 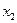 , ¼,
, ¼, 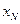 , попавший в
, попавший в 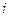 –й отрезок
–й отрезок 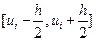 (если какая-либо точка выборки попала в одну из граничных точек, общую сразу для двух отрезков, то можно условиться отнести ее к левому отрезку разбиения). Число
(если какая-либо точка выборки попала в одну из граничных точек, общую сразу для двух отрезков, то можно условиться отнести ее к левому отрезку разбиения). Число 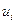 называется
называется 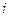 –й вариантой выборки, а число
–й вариантой выборки, а число 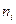 - частотой этой варианты. По построению,
- частотой этой варианты. По построению, 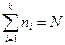 . Таблица
. Таблица
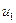 | 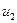 | 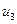 | ¼ | 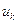 |
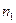 | 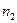 | 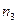 | ¼ | 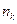 |
называется вариационным рядом. Переход от первичной выборки к вариационному ряду позволяет, во-первых, уменьшить объем вычислений при обработке информации, а, во-вторых, уменьшить влияние случайных ошибок за счет усреднения экспериментальных данных.
 Величина
Величина 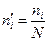 называется относительной частотой варианты
называется относительной частотой варианты 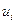 , а величина
, а величина 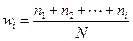 называется ее накопленной частотой. В статистике приняты два основных способа графического изображения данных – гистограмма и полигон. В первом случае график функции (как непрерывного, так и дискретного аргумента) изображается в виде системы прямоугольников, в основании которых лежат отрезки разбиения
называется ее накопленной частотой. В статистике приняты два основных способа графического изображения данных – гистограмма и полигон. В первом случае график функции (как непрерывного, так и дискретного аргумента) изображается в виде системы прямоугольников, в основании которых лежат отрезки разбиения 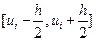 , а высота равна значению соответствующей функции на данном отрезке. Полигон представляет собой ломаную линию, вершины которой лежат в точках с абсциссами
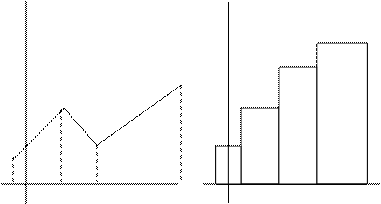
, а высота равна значению соответствующей функции на данном отрезке. Полигон представляет собой ломаную линию, вершины которой лежат в точках с абсциссами 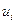 . Приведем для примера полигон относительных частот и гистограмму накопленных частот.
. Приведем для примера полигон относительных частот и гистограмму накопленных частот.
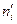
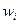
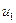
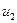
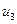
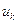
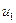
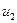
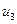
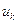
Полигон или гистограмма относительных частот является статистическим аналогом функции плотности распределения. Полигон или гистограмма накопленных частот является аналогом функции распределения генеральной совокупности.
Зная вариационный ряд, можно определить точечную оценку математического ожидания генеральной совокупности. Эта оценка называется выборочным средним 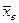 и определяется формулой
и определяется формулой
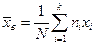 .
.
Точечная оценка дисперсии генеральной совокупности 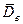 , называемая выборочной дисперсией, определяется формулой
, называемая выборочной дисперсией, определяется формулой
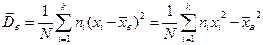 .
.
Величину 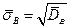 называют выборочным средне квадратичным уклонением. Оценка
называют выборочным средне квадратичным уклонением. Оценка 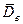 является состоятельной, но смещенной. Соответствующая несмещенная оценка для дисперсии обозначается
является состоятельной, но смещенной. Соответствующая несмещенная оценка для дисперсии обозначается 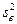 и определяется формулой
и определяется формулой
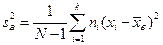 .
.
Приведем пример интервальной оценки параметров генеральной совокупности. Предположим, что среднее квадратичное уклонение 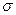 генеральной совокупности известно (на практике его принимают равным
генеральной совокупности известно (на практике его принимают равным 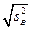 ). Тогда доверительный интервал, которому с вероятностью, не меньшей
). Тогда доверительный интервал, которому с вероятностью, не меньшей 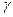 , принадлежит математическое ожидание генеральной совокупности, определяется формулой
, принадлежит математическое ожидание генеральной совокупности, определяется формулой
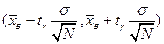 ,
,
где 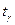 - решение уравнения
- решение уравнения
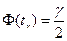 .
.
Здесь, как и раньше, 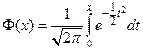 – функция Лапласа. Решают это уравнение численно, при помощи той же таблицы, в которой приведены значения функции
– функция Лапласа. Решают это уравнение численно, при помощи той же таблицы, в которой приведены значения функции 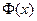 при различных значениях аргумента
при различных значениях аргумента 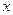 .
.
Рассмотрим процедуру проверки гипотезы о нормальном распределении генеральной совокупности. Построив график эмпирических относительных частот, который является аналогом функции плотности распределения, можно “наложить” на этот график функцию плотности нормального закона 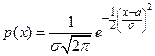 с показателями
с показателями 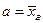 ,
, 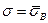 . Если видимые уклонения графика эмпирической функции плотности от графика теоретической функции плотности не слишком значительны, то можно высказать гипотезу о том, что генеральная совокупность распределена по нормальному закону. Такая гипотеза, однако, нуждается в подтверждении на основании того или иного измерения уклонения одного графика от другого. Изложим критерий Пирсона, который позволяет подтвердить или опровергнуть данную гипотезу с заданным уровнем значимости
. Если видимые уклонения графика эмпирической функции плотности от графика теоретической функции плотности не слишком значительны, то можно высказать гипотезу о том, что генеральная совокупность распределена по нормальному закону. Такая гипотеза, однако, нуждается в подтверждении на основании того или иного измерения уклонения одного графика от другого. Изложим критерий Пирсона, который позволяет подтвердить или опровергнуть данную гипотезу с заданным уровнем значимости 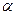 . Начнем с объяснения, что такое уровень значимости гипотезы. Поскольку в выборке содержится неполная информация о генеральной совокупности, какое бы решение мы не приняли - принять гипотезу или отвергнуть, мы можем сделать ошибку. Ошибкой первого рода является отказ от гипотезы в том случае, когда она на самом деле верна. Вероятность ошибки первого рода называется уровнем значимости гипотезы. Ошибкой второго рода считается принятие гипотезы, в случае, когда утверждение гипотезы неверно. Вероятность не сделать ошибку второго рода называют мощностью критерия. Пусть уровень значимости гипотезы о нормальном законе распределения задан и равен
. Начнем с объяснения, что такое уровень значимости гипотезы. Поскольку в выборке содержится неполная информация о генеральной совокупности, какое бы решение мы не приняли - принять гипотезу или отвергнуть, мы можем сделать ошибку. Ошибкой первого рода является отказ от гипотезы в том случае, когда она на самом деле верна. Вероятность ошибки первого рода называется уровнем значимости гипотезы. Ошибкой второго рода считается принятие гипотезы, в случае, когда утверждение гипотезы неверно. Вероятность не сделать ошибку второго рода называют мощностью критерия. Пусть уровень значимости гипотезы о нормальном законе распределения задан и равен 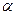 . Уклонение эмпирической функции плотности от теоретической определяется величиной
. Уклонение эмпирической функции плотности от теоретической определяется величиной
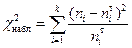 .
.
Здесь 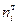 - теоретическая частота
- теоретическая частота 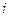 -го интервала. Она равняется среднему числу попаданий случайной величины распределенной по нормальному закону с данными показателями
-го интервала. Она равняется среднему числу попаданий случайной величины распределенной по нормальному закону с данными показателями 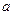 и
и 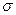 из общего числа в
из общего числа в 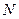 испытаний:
испытаний:
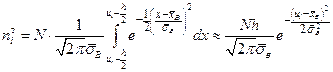 .
.
Случайная величина, реализацией которой является число 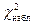 , имеет так называемое распределение
, имеет так называемое распределение 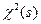 . Эта случайная величина зависит от некоторого целого параметра
. Эта случайная величина зависит от некоторого целого параметра 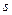 , называемого числом степеней свободы распределения. В данном случае число степеней свободы равно
, называемого числом степеней свободы распределения. В данном случае число степеней свободы равно 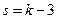 , где
, где 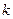 – число интервалов разбиения выборки. Критические точки распределения
– число интервалов разбиения выборки. Критические точки распределения 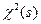 (то есть решения уравнения
(то есть решения уравнения 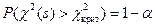 ) при различных значениях
) при различных значениях 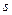 ,
, 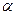 затабулированы в виде значений функции
затабулированы в виде значений функции 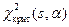 . Таким образом, при заданном уровне значимости
. Таким образом, при заданном уровне значимости 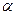 и известном числе
и известном числе 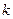 интервалов группировки мы можем найти пороговое значение
интервалов группировки мы можем найти пороговое значение 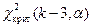 превышение которого заставляет нас отвергнуть гипотезу о нормальном распределении генеральной совокупности. Иными словами, если
превышение которого заставляет нас отвергнуть гипотезу о нормальном распределении генеральной совокупности. Иными словами, если 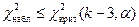 , то на заданном уровне значимости
, то на заданном уровне значимости 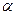 гипотезу о нормальном распределении генеральной совокупности можно считать не противоречащей экспериментальным данным. Если
гипотезу о нормальном распределении генеральной совокупности можно считать не противоречащей экспериментальным данным. Если 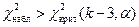 , то гипотезу о нормальном распределении отвергают.
, то гипотезу о нормальном распределении отвергают.
Задача 5.6. Для выборки объема N =100, представленной вариационным рядом
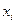 | -1 | ||||||
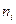 |
построить полигон относительных частот и гистограмму накопленных частот. Найти выборочное среднее 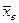 и выборочное среднее квадратичное уклонение
и выборочное среднее квадратичное уклонение 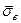 . Определить доверительный интервал с доверительной вероятностью b =0.95 для оценки математического ожидания генеральной совокупности в предположении, что среднее квадратичное уклонение генеральной совокупности s равно исправленному выборочному среднему s. Проверить гипотезу о нормальности закона распределения генеральной совокупности, используя критерий Пирсона с уровнем значимости a =0.05.
. Определить доверительный интервал с доверительной вероятностью b =0.95 для оценки математического ожидания генеральной совокупности в предположении, что среднее квадратичное уклонение генеральной совокупности s равно исправленному выборочному среднему s. Проверить гипотезу о нормальности закона распределения генеральной совокупности, используя критерий Пирсона с уровнем значимости a =0.05.
Решение. Выпишем относительные и накопленные частоты по данной выборке.
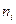 | |||||||
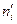 | 0.03 | 0.12 | 0.1 | 0.15 | 0.42 | 0.13 | 0.05 |
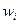 | 0.03 | 0.15 | 0.25 | 0.40 | 0.82 | 0.95 |
Построим полигон относительных частот  .
.
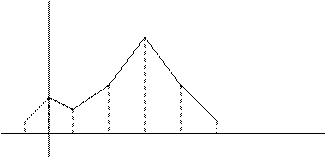
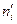
0.42
0.25
0.15
0.05
 0 1 2 3 4 5
0 1 2 3 4 5
 Построим гистограмму накопленных частот.
Построим гистограмму накопленных частот.
0.95
0.82
0.40
0.25
0.15
0.03
 0 1 2 3 4 5
0 1 2 3 4 5
Найдем выборочное среднее.
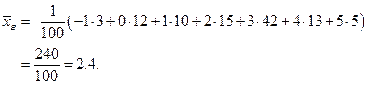
Найдем выборочную дисперсию
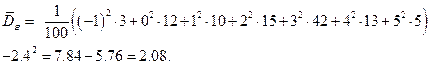 Выборочное среднее квадратичное равно
Выборочное среднее квадратичное равно
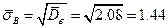 .
.
Исправленная выборочная дисперсия равна
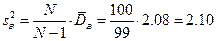 ,
,
откуда
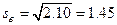 .
.
Найдем доверительный интервал для математического ожидания с доверительной вероятностью b =0.95 с предположении, что среднее квадратичное уклонение генеральной совкупности 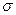 равно
равно 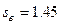 .
.
Из таблицы значений функции Лапласа находим, что решение уравнения 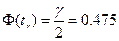 равно
равно 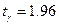 , откуда доверительный интервал равен
, откуда доверительный интервал равен
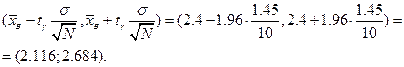
Самая трудоемкая часть задачи состоит в проверки гипотезы о нормальности закона распределения генеральной совокупности с использованием критерий Пирсона с уровнем значимости a =0.05
Найдем теоретические частоты
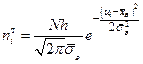
для данного вариационного ряда. Результаты подсчета запишем в виде таблицы. Коэффициент 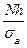 равен
равен 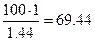 . Обозначим
. Обозначим 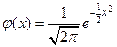 плотность стандартного нормального распределения. Функция
плотность стандартного нормального распределения. Функция 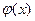 затабулирована, и нам нужно лишь определить значения ее аргумента
затабулирована, и нам нужно лишь определить значения ее аргумента 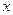 в точках
в точках 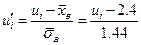 . Далее,
. Далее, 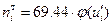 .
.
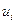 | 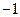 | ||||||
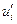 | 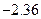 | 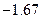 | 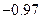 | 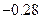 | 0.42 | 1.11 | 1.81 |
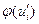 | 0.024 | 0.099 | 0.249 | 0.384 | 0.366 | 0.215 | 0.078 |
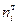 | 1.7 | 6.9 | 17.3 | 26.7 | 25.4 | 5.4 |
Теперь мы можем определить 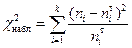 .
.
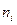 | |||||||
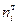 | 1.7 | 6.9 | 17.3 | 26.7 | 25.4 | 5.4 | |
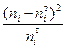 | 0.99 | 3.77 | 3.08 | 5.13 | 10.85 | 0.27 | 0.03 |
Следовательно, 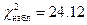 . Определим
. Определим 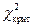 . Число степеней свободы равно
. Число степеней свободы равно 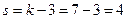 . Уровень значимости
. Уровень значимости 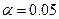 . По таблице критических точек распределения
. По таблице критических точек распределения 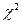 находим
находим 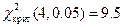 . Поскольку
. Поскольку 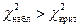 гипотезу о нормальном законе распределения генеральной совокупности следует отвергнуть.
гипотезу о нормальном законе распределения генеральной совокупности следует отвергнуть.
Многомерные выборки. Функции регрессии.
При проведении статистического эксперимента мы можем фиксировать результаты измерений двух или более характеристик эксперимента (случайных величин). При этом мы можем изучать как параметры каждой случайной величины в отдельности, так и совместное распределение этих случайных величин. Одним из важнейших вопросов является определение зависимости одной из случайных величин от другой. Ограничимся случаем двумерной выборки.
Пусть в результате статистического эксперимента получена двумерная выборка данных объема 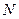 :
: 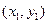 ,
, 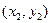 ,
, 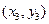 , ¼,
, ¼, 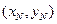 . Разобьем интервал, в который попали координаты
. Разобьем интервал, в который попали координаты 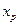 наблюдаемых пар на
наблюдаемых пар на 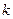 отрезков с серединами
отрезков с серединами 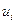 ,
, 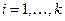 . Интервал, в который попали координаты
. Интервал, в который попали координаты 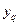 , разобьем на
, разобьем на 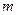 отрезков с серединами
отрезков с серединами 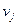 ,
, 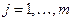 . Пусть в прямоугольник, в основании которого лежит
. Пусть в прямоугольник, в основании которого лежит 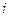 -й отрезок разбиения по оси
-й отрезок разбиения по оси 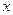 , а вторая сторона отвечает
, а вторая сторона отвечает 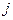 –му отрезку разбиения по оси
–му отрезку разбиения по оси 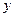 , попало
, попало 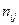 пар точек наблюдений. Мы приходим к двумерному вариационному ряду, вариантами которого являются пары
пар точек наблюдений. Мы приходим к двумерному вариационному ряду, вариантами которого являются пары 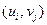 с частотами
с частотами 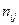 ,
, 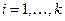 ,
, 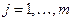 .
.
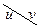 | 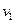 | ¼ | 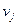 | ¼ | 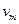 |
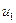 | 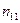 | ¼ | 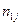 | ¼ |  |
 |  |  |  |  |  |
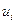 | 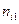 | ¼ | 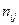 | 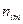 | |
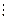 | 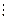 | 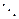 | 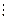 | 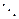 | 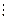 |
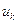 | 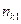 | ¼ | 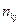 | ¼ | 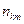 |
По данному двумерному вариационному ряду нетрудно построить вариационные ряда для величин 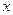 и
и 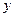 в отдельности, после чего найти выборочные средние
в отдельности, после чего найти выборочные средние 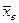 ,
, 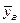 и выборочные средне квадратичные уклонения
и выборочные средне квадратичные уклонения 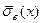 ,
, 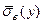 .
.
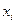 | 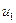 | 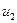 | 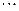 | 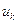 |
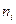 | 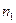 | 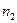 | 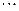 | 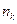 |
где 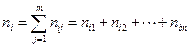 . Аналогично,
. Аналогично,
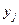 | 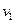 | 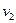 |  | 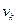 |
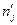 | 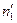 | 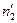 | 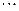 | 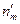 |
где 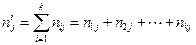 . Отметим, что
. Отметим, что
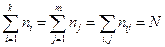 .
.
Наша цель заключается в установлении зависимости величины 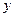 от
от 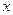 , которая в каком-то смысле точнее всего соответствовала бы экспериментальным данным. Определим условное выборочное среднее
, которая в каком-то смысле точнее всего соответствовала бы экспериментальным данным. Определим условное выборочное среднее 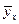 при заданном значении
при заданном значении 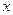 :
:
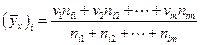 ,
, 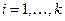 .
.
В результате получаем 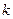 точек
точек
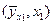 ,
, 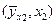 , ¼,
, ¼, 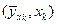
плоскости 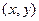 с весами
с весами 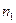 ,
, 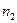 , ¼,
, ¼, 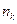 . Найдем такую линейную функцию
. Найдем такую линейную функцию 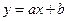 , для которой совокупное расстояние до всех точек
, для которой совокупное расстояние до всех точек 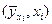 , измеряемое функцией
, измеряемое функцией
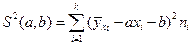 ,
,
было бы наименьшим (принцип наименьших квадратов Гаусса). Разрешая систему уравнений
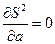 ,
, 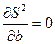 ,
,
относительно 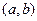 , запишем уравнение линейной регрессии в виде
, запишем уравнение линейной регрессии в виде
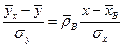 ,
,
где
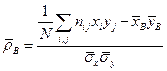
есть выборочный коэффициент корреляции.
Задача 5.7. По выборке объема N =100 двумерной генеральной совокупности, представленной таблицей
 | 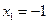 | 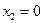 | 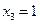 | 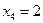 | 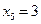 | 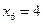 | 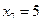 |
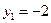 | |||||||
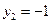 | |||||||
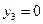 | |||||||
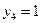 | |||||||
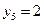 |
написать уравнение линейной регрессии для условного математического ожидания 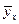 на x в виде
на x в виде 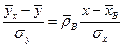 где
где 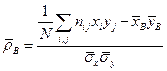 . Сделать схематический чертеж.
. Сделать схематический чертеж.
Решение. Выпишем одномерные выборки для величин 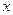 ,
, 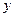 .
.
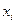 | 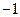 | 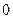 |  | ||||
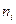 |
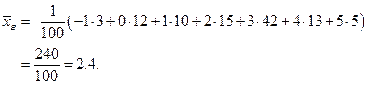
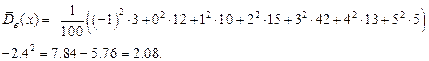
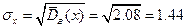 .
.
Аналогично,
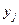 | 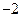 | 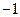 | |||
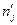 |
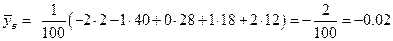 .
.
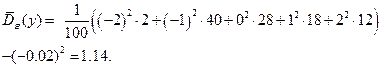
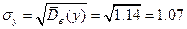 .
.
Для определения уравнения регрессии осталось вычислить выборочный коэффициент корреляции 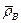 . Найдем сумму
. Найдем сумму
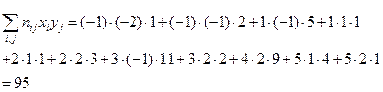
Подставляем найденное значение суммы смешанных произведений в формулу выборочного коэффициента корреляции
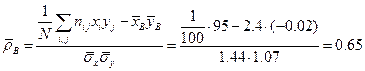 .
.
Уравнение линейной регрессии 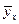 на
на 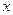 имеет вид
имеет вид
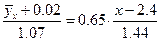 Û
Û 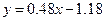 .
.
Сделаем схематический чертеж. Для этого выпишем условные выборочные средние 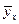 при
при 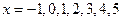 .
.
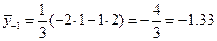 ,
,
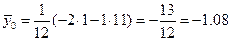 ,
,
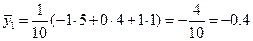 ,
,
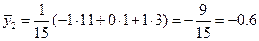 ,
,
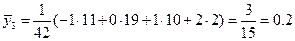 ,
,
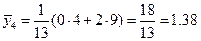 ,
,
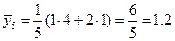 .
.
Теперь построим на одной координатной плоскости график функции 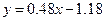 и точки
и точки 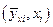 .
.

 2015-05-13
2015-05-13 3243
3243
