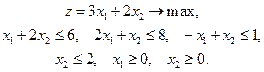
Записываем систему ограничений в виде уравнений:
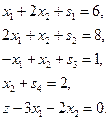
Полученные уравнения записываем в виде симплекс-таблицы:
| Б | 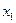 | 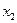 | 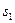 | 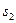 | 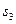 | 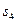 | ||
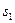 | 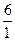 | |||||||
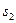 | 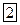 | 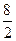 | ||||||
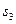 | -1 | ¾ | ||||||
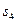 | ¾ | |||||||
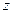 | -3 | -2 |
Ö
Опорный план найден. Базисные переменные 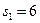 ,
, 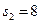 ,
, 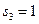 ,
, 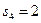 . Свободные переменные
. Свободные переменные 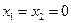 . Значение
. Значение 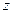 в точке опорного плана равно 0. План не оптимален, поскольку в
в точке опорного плана равно 0. План не оптимален, поскольку в 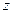 –строке имеются отрицательные коэффициенты. Для улучшения опорного плана проведем жорданово преобразование, выбрав в качестве разрешающего столбца столбец №1. Чтобы определить разрешающую строку, найдем отношения элементов свободного столбца и соответствующих элементов разрешающего столбца и выберем ту строку, в которой соответствующее отношение неотрицательно и минимально. В результате получаем строку №2. Таким образом, мы заменяем базисную переменную
–строке имеются отрицательные коэффициенты. Для улучшения опорного плана проведем жорданово преобразование, выбрав в качестве разрешающего столбца столбец №1. Чтобы определить разрешающую строку, найдем отношения элементов свободного столбца и соответствующих элементов разрешающего столбца и выберем ту строку, в которой соответствующее отношение неотрицательно и минимально. В результате получаем строку №2. Таким образом, мы заменяем базисную переменную 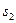 на переменную
на переменную 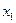 .
.
1-я итерация жорданова преобразования.
| Б | 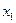 | 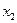 | 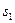 | 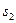 | 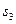 | 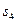 | ||
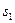 | 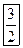 | 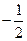 | 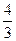 | |||||
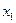 | 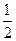 | 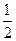 | ||||||
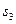 | 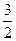 | 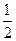 | 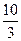 | |||||
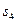 | ||||||||
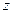 | - 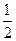 | 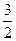 |
Ö
Вновь опорный план не оптимален. Разрешающий столбец теперь определен однозначно – это столбец №2. Минимальное отношение элементов свободного столбца и разрешающего столбца достигается в строке №1. Теперь базисную переменную 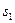 мы заменяем на переменную
мы заменяем на переменную 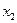 .
.
2-я итерация жорданова преобразования.
| Б | 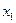 | 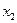 | 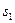 | 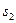 | 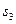 | 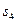 | |
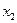 | 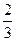 | 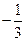 | 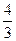 | ||||
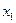 | 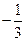 | 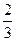 | 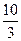 | ||||
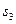 | -1 | ||||||
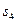 | 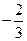 | 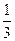 | 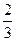 | ||||
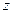 | 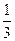 | 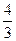 | 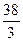 |
Поскольку в целевой строке нет отрицательных элементов, полученный план оптимален. Значения базисных переменных 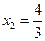 ,
, 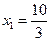 ,
, 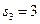 ,
, 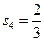 . Значения свободных переменных
. Значения свободных переменных 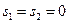 , максимальное значение целевой функции
, максимальное значение целевой функции 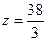 .
.
Задача 6.2. Фирма выпускает три вида продукции. В процессе производства используется три технологические операции. В таблице для каждой операции указано, сколько времени занимает ее выполнение в процессе изготовления 1 единицы продукции каждого вида. В той же таблице указан суммарный фонд рабочего времени, в течение которого могут проводиться технологические операции.
| Операция | Время на 1 изделие (мин/шт) | Общий ресурс времени (час) | ||
| продукт №1 | Продукт №2 | продукт №3 | ||
| I | ||||
| II | ||||
| III |
Ожидаемая прибыль от продажи одного изделия каждого вида составляет 5, 7 и 12 рублей соответственно. Определите наиболее выгодный суточный объем производства каждого вида продукции.
Решение. Обозначим 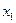 ,
, 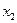 ,
, 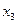 количество единиц каждого из трех видов продукции. Тогда общее время, необходимое для выполнения такого плана, распределяется по каждой из трех операций следующим образом. Операция №1 выполняется в течение
количество единиц каждого из трех видов продукции. Тогда общее время, необходимое для выполнения такого плана, распределяется по каждой из трех операций следующим образом. Операция №1 выполняется в течение 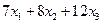 минут, операция №2 выполняется в течение
минут, операция №2 выполняется в течение 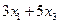 минут, операция №3 выполняется в течение
минут, операция №3 выполняется в течение 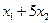 минут. С учетом того, что ресурс времени по операциям равен соответственно 1440, 1200 и 1080 минутам, получаем ограничения на возможные значения плана производства
минут. С учетом того, что ресурс времени по операциям равен соответственно 1440, 1200 и 1080 минутам, получаем ограничения на возможные значения плана производства
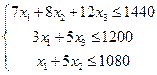
Прибыль от продажи продукции составит 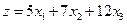 рублей. Следовательно, математическая формулировка задачи имеет вид:
рублей. Следовательно, математическая формулировка задачи имеет вид:
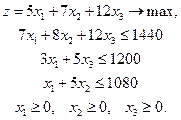
Запишем задачу линейного программирования в стандартной форме.
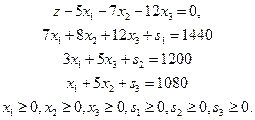
Запишем систему уравнений в виде симплекс таблицы.
| Б | 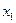 | 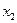 | 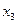 | 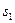 | 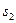 | 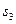 | ||
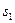 | 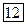 | 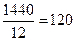 | ||||||
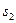 | 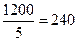 | |||||||
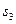 | ¾ | |||||||
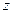 | -3 | -7 | -12 |
Ö
У нас имеется три базисные переменные - 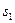 ,
, 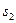 ,
, 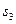 . Следовательно, опорный план найден. Поскольку
. Следовательно, опорный план найден. Поскольку 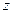 -строка имеет отрицательные коэффициенты, опорный план не оптимален. Выберем самый большой по модулю отрицательный коэффициент
-строка имеет отрицательные коэффициенты, опорный план не оптимален. Выберем самый большой по модулю отрицательный коэффициент 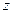 -строки (-12) и назначим разрешающим столбцом третий столбец симплекс таблицы. Чтобы выбрать разрешающую строку, составим отношения элементов свободного и разрешающего столбцов:
-строки (-12) и назначим разрешающим столбцом третий столбец симплекс таблицы. Чтобы выбрать разрешающую строку, составим отношения элементов свободного и разрешающего столбцов: 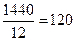 ,
, 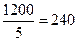 (а для третьей строки это отношение отрицательно и потому опускается). Выберем минимальное положительное отношение. Оно равно 120 и достигается в первой строке. Следовательно, в качестве разрешающей строки следует выбрать строку №1. Проведем полное жорданово исключение переменной
(а для третьей строки это отношение отрицательно и потому опускается). Выберем минимальное положительное отношение. Оно равно 120 и достигается в первой строке. Следовательно, в качестве разрешающей строки следует выбрать строку №1. Проведем полное жорданово исключение переменной 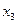 с помощью первой строки симплекс-таблице. В результате базисную переменную
с помощью первой строки симплекс-таблице. В результате базисную переменную 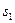 заменим на свободную переменную
заменим на свободную переменную 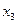 .
.
| Б | 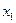 | 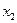 | 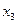 | 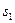 | 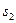 | 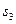 | |
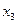 | 7/12 | 2/3 | 1/12 | ||||
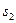 | 1/12 | -10/3 | -5/12 | ||||
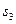 | |||||||
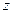 |
Новый опорный план: 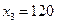 ,
, 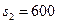 ,
, 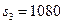 ,
, 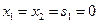 ,
, 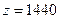 . Поскольку все элементы
. Поскольку все элементы 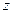 -строки неотрицательны, план оптимален. Вспомогательные переменные
-строки неотрицательны, план оптимален. Вспомогательные переменные 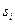 интерпретируются как остатки ресурсов. В частности, первый ресурс является дефицитным и расходуется полностью, поскольку его остаток
интерпретируются как остатки ресурсов. В частности, первый ресурс является дефицитным и расходуется полностью, поскольку его остаток 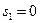 . Второй и третий ресурсы являются избыточными и их остатки равны
. Второй и третий ресурсы являются избыточными и их остатки равны 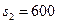 ,
, 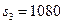 .
.
 2015-05-13
2015-05-13 771
771








