Дадим сначала определение преобразования системы линейных уравнений методом полного жорданова исключения. Пусть имеется система 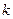 линейных уравнений с
линейных уравнений с 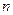 неизвестными
неизвестными
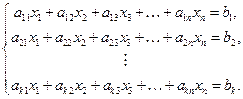
Сопоставим системе уравнений следующую симплекс-таблицу
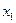
| 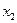
| 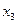
| ¼ | 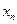
| |
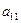
| 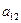
| 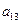
| 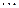
| 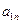
| 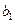
|
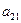
| 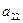
| 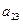
| 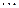
| 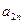
| 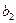
|
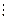
| 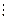
| 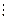
| 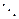
| 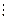
| |
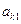
| 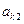
| 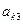
| 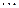
| 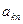
| 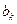
|
Назовем полным жордановым исключением переменной 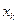 с помощью
с помощью 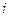 –го уравнения следующее эквивалентное преобразование симплекс-таблицы данной системы уравнений. Строку с номером
–го уравнения следующее эквивалентное преобразование симплекс-таблицы данной системы уравнений. Строку с номером 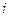 назовем разрешающей строкой. Столбец с номером
назовем разрешающей строкой. Столбец с номером 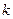 назовем разрешающим столбцом. Элемент, стоящий на пересечении разрешающей строки и столбца, назовем разрешающим элементом.
назовем разрешающим столбцом. Элемент, стоящий на пересечении разрешающей строки и столбца, назовем разрешающим элементом.
Шаг 1. Перепишем разрешающую строку без изменений, дополним разрешающий столбец нулями.
Шаг 2. Элементы остальных строк и столбцов преобразуем по правилу прямоугольника. Соединим элемент 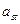 таблицы с разрешающим элементом
таблицы с разрешающим элементом 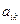 и достроим полученную диагональ до прямоугольника. Теперь заменим
и достроим полученную диагональ до прямоугольника. Теперь заменим 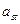 на разность произведения элементов
на разность произведения элементов 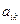 и
и 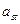 и произведения элементов
и произведения элементов 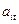 и
и 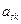 :
:


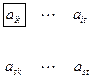 ®
® 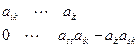
Шаг 3. Поделим полученную таблицу на разрешающий элемент 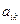 .
.
Пример. 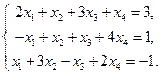
Проведем полное жорданово исключение переменой 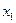 с помощью первого уравнения. Запишем систему в виде симплекс-таблицы.
с помощью первого уравнения. Запишем систему в виде симплекс-таблицы.
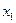
| 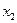
| 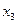
| 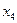
| |
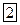
| ||||
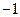
| ||||
| -1 | -1 |
В качестве разрешающего элемента выбираем элемент первой строки и первого столбца системы.
Шаг 1. Перепишем разрешающую строку без изменений, дополним разрешающий столбец нулями.
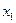
| 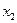
| 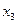
| 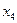
| |
Шаг 2. Остальные элементы преобразуем по правилу прямоугольника. Для элементов второй строки последовательно получаем:
1 ® 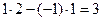
1 ® 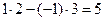
4 ® 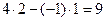
1 ® 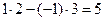
Для элементов третьей строки получаем
3 ® 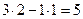
-1 ® 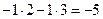
2 ® 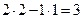
-1 ® 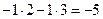
В результате получим
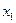
| 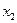
| 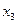
| 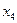
| |
| -5 | -5 |
Шаг 3. Поделим полученную таблицу на разрешающий элемент.
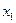
| 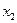
| 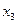
| 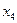
| |
| 1/2 | 3/2 | 1/2 | 3/2 | |
| 3/2 | 5/2 | 9/2 | 5/2 | |
| 5/2 | -5/2 | 3/2 | -5/2 |
На этом преобразование жорданова исключения закончено.
Задача линейного программирования в стандартной форме записывается в следующем виде. Требуется найти максимальное значение функции 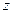 ,
,
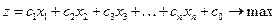
при ограничениях
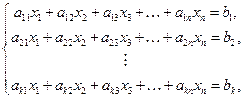
в предположении, что все переменные неотрицательны
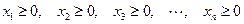
При этом все свободные переменные в правой части уравнений предполагаются также неотрицательными, 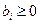 .
.
 2015-05-13
2015-05-13 705
705








