Задача 1. В двух капиллярных трубках разного диаметра, опущенных в воду, установилась разность уровней 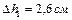 . При опускании этих же трубок в спирт разность уровней оказалась
. При опускании этих же трубок в спирт разность уровней оказалась 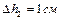 . Зная коэффициент поверхностного натяжения воды
. Зная коэффициент поверхностного натяжения воды 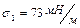 , найти коэффициент поверхностного натяжения спирта
, найти коэффициент поверхностного натяжения спирта 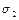 .
.
Решение
Высота подъема жидкости в капилляре определяется по формуле
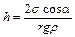 ,
,
где 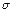 - коэффициент поверхностного натяжения,
- коэффициент поверхностного натяжения, 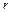 - радиус капилляра,
- радиус капилляра, 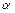 - краевой угол,
- краевой угол,  - плотность жидкости. Полагая смачивание полным (
- плотность жидкости. Полагая смачивание полным (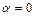 ), находим для двух капилляров в случае воды
), находим для двух капилляров в случае воды
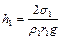 ,
, 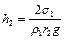 ,
,
следовательно, разность уровней
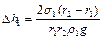 . (2.4.1)
. (2.4.1)
Аналогичные расчеты в случае спирта дают
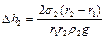 . (2.4.2)
. (2.4.2)
Из (2.4.1), (2.4.2) находим
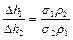 .
.
Отсюда коэффициент поверхностного натяжения ртути
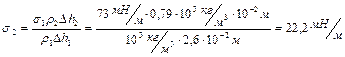 .
.
Задача 2. Капля ртути массой 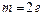 введена между параллельными стеклянными пластинами. Какую силу следует приложить, чтобы расплющить каплю до толщины
введена между параллельными стеклянными пластинами. Какую силу следует приложить, чтобы расплющить каплю до толщины 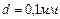 . Считать, что ртуть не смачивает стекло.
. Считать, что ртуть не смачивает стекло.
Решение
Если жидкость не смачивает твердое тело, то давление под поверхностью жидкости оказывается больше внешнего давления на величину, определяемую по формуле Лапласа
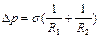 , (2.4.3)
, (2.4.3)
где 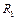 и
и 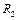 - радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости.
- радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости.
Сечение капли плоскостью, перпендикулярной пластинам и проходящей через центр капли представляет собой фигуру, две стороны которой прямолинейны и параллельны, а две другие – окружности радиусом 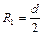 . Сечение капли плоскостью, параллельной пластинам дает окружность радиусом
. Сечение капли плоскостью, параллельной пластинам дает окружность радиусом 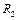 , найти который можно, вычисляя приближенно (пренебрегая криволинейностью свободной поверхности) объем капли.
, найти который можно, вычисляя приближенно (пренебрегая криволинейностью свободной поверхности) объем капли.
Получаем
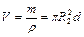 ,
,
откуда следует
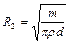 . (2.4.4)
. (2.4.4)
Из (2.4.3), (2.4.4) находим
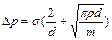 .
.
Следовательно, сила давления на пластины равна
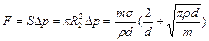 .
.
Подставляя значения, получаем

 2015-05-13
2015-05-13 2655
2655








