Л.М.Мартынов. Вводный курс математики, стр.109-129.
1. Сформулируйте правило суммы.
2. Сформулируйте правило произведения.
3. Определите составление каких соединений (перестановок, сочетаний или размещений) происходит в каждом из следующих случаев:
а) образование упорядоченных подмножеств;
б) образование подмножеств, состоящее в выделении из данного множества некоторой части его элементов;
в) образование упорядоченных подмножеств, состоящее в установлении определенного порядка следования элементов множества друг за другом.
4. Сформулируйте правило: как найти число размещений из n элементов по k(k≤n) без повторений – и напишите соответствующую формулу.
5. Сформулируйте правило: как найти число сочетаний из n элементов по k(k≤n) – и напишите соответствующую формулу.
6. Что называется факториалом числа n?
7. Сформулируйте правило: как найти число всевозможных перестановок из n элементов– и напишите соответствующую формулу.
8. Чему равно число размещений из n элементов по k с повторениями?
|
|
|
9. Чему равно число сочетаний из n элементов по k с повторениями?
10. Чему равно число перестановок с повторениями порядка n, имеющих состав (n1, n2,…, nk)?
11. Используя арифметический треугольник (треугольник Паскаля) найдите биномиальные коэффициенты в разложении (x+y)8.
Разберите решения следующих примеров.
П р и м е р 1. В корзине 6 яблок, 4 груши, 7 мандаринов и 3 апельсина. Сколькими способами можно выбрать один фрукт?
Решение. По правилу суммы: 6+4+7+3=20 способами.
П р и м е р 2. На каникулы школьник получил задание: выучить доказательство любой из шести теорем, прочитать один из семи романов, написать сочинение на одну из четырех тем. Сколькими способами можно выполнить задание?
Решение. По правилу произведения: 6∙7∙4=108 способами.
П р и м е р 3.Спортлото «5 из 36». Из 36 клеток на карточке зачеркивают 5. Сколькими способами можно заполнить карточку?
Решение. Исходы этого эксперимента можно интерпретировать как образование подмножеств, содержащих 5 элементов, из 36-элементного множества (порядок элементов не важен, а состав (выбор) элементов важен). Следовательно, по формуле числа сочетаний (без повторений) получаем
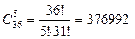 .
.
П р и м е р 4. В отделе 7 сотрудников, включая начальника. Из них решено выбрать тройку – делегацию на научно-практическую конференцию. Сколькими способами это можно сделать?
Решение. Различные тройки должны отличаться хотя бы одним делегатом. Значит, ответом на вопрос будет число сочетаний из семи элементов по три: 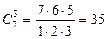
П р и м е р 4а. Сколько различных троек (делегаций) включают начальника отдела и сколько – не включают?
Решение. Если начальник – один из делегатов, то еще двои можно выбирать из остальных шести сотрудников отдела; для этого существует 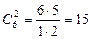 способов.
способов.
|
|
|
Если же начальник не входит в делегацию, то всех троих делегатов придется выбирать из шести сотрудников (кроме самого начальника) Для этого существует 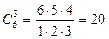 способов.
способов.
Замечание: Итак, делегаций включающих начальника отдела, существует 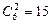 , не включающих начальника
, не включающих начальника 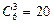 . Таким образом, общее число делегаций, равное
. Таким образом, общее число делегаций, равное 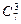 разбилось на 2 группы, а именно
разбилось на 2 группы, а именно 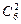 и
и 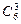 . Значит,
. Значит, 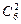 +
+ 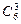 =
= 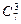
Если бы в составе отдела было n сотрудников, а в делегацию избирали k человек, то дословно повторив наше рассуждение, мы получили бы общую формулу, которую иногда называют правило Паскаля: 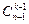 +
+ 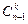 =
= 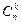
П р и м е р 5. Спортпрогноз. Пусть, например, требуется назвать тройку призеров чемпионата России по футболу (18 команд). Сколькими способами это можно сделать?
Решение. Кроме того, что различные тройки должны отличаться составом, они отличаются и порядком («Спартак» на первом месте, а «Зенит» на втором или наоборот – это соответствует разным тройкам призеров), причем эти упорядоченные тройки без повторений (на каждое место ставится одна команда). Число всех способов назвать тройку призеров составляет 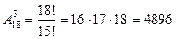
П р и м е р 6. Сколько различных трехзначных чисел можно составить из цифр 1,2,3,4,5,7,9 так, чтобы цифры не повторялись
Решение. Сгруппируем (столбцами) числа, записанные одними и теми же цифрами:
| . | . | . | |||||||||||||
| . | . | . | |||||||||||||
| . | . | . | |||||||||||||
В каждом столбце ровно 6 различных трехзначных чисел, составленных из одних и тех же цифр, но в различном порядке (объясните, почему именно 6). Эти трехзначные числа отличаются друг от друга либо выбором цифр в различных столбцах, либо порядком их расположения в одном и том же столбце. Как известно, такие соединения называются размещенными; значит для ответа на вопрос задачи, нужно найти число размещений из 7 элементов по 3: 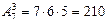 .
.
П р и м е р 7. Сколько различных произведений по 3 сомножителя можно составить, используя числа 1,2,3,4,5,7,9 в качестве сомножителей?
Решение. Воспользуемся написанными в предыдущем примере столбцами. Одно из возможных произведений будет 1∙2∙3; все другие произведения, записанные по образцу этого же столбца (1∙2∙3 и т.д.) отличаются лишь порядком множителей и, следовательно, не являются различными произведениями. Различных же произведений будет столько, сколько выше было столбцов, т.е. во столько раз меньше, чем различных трехзначных чисел, сколькими способами можно переставлять эти три цифры. Значит, ответ на вопрос получается делением 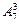 на
на 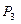 , т.е.
, т.е. 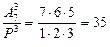 . Ответ можно было получить и по формуле
. Ответ можно было получить и по формуле 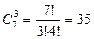 , т.к. речь в этой задаче шла о различных трехэлементных неупорядоченных подмножествах, входящих в множество из семи элементов 1,2,3,4,5,7,9.
, т.к. речь в этой задаче шла о различных трехэлементных неупорядоченных подмножествах, входящих в множество из семи элементов 1,2,3,4,5,7,9.
Замечание. Если бы в этом примере в качестве сомножителей были и числа 6 и 8, то разные сомножители могли бы дать одно и то же произведение (например, 1∙8 = 2∙4, 2∙6 = 3∙4 и т.д.), так что подсчет числа различных произведений был бы сложен.
П р и м е р 8.Сколько «слов» можно получить, переставляя буквы О,П,Р,С,Т?
Решение. Переставляя буквы, получаем упорядоченные множества, которые отличаются друг от друга лишь порядком входящих в них букв. Имеем дело с перестановками без повторений, следовательно, «слов» получится P5 = 5! = 1∙2∙3∙4∙5 = 120.
П р и м е р 9. Катя, Таня и Оля подошли к скамейке. Сколькими способами они могут усесться на ней?
|
|
|
Решение. 1 способ. Решим эту задачу, опираясь на графы – именно они при решении комбинаторных задач позволяют приучиться к полному перебору всех возможных вариантов (заметим, что этот способ изложения позволяет вести занятия по комбинаторике и для школьников 7-8 классов).
Возьмем заглавные буквы имен девочек. Здесь нужно найти число размещений трех девочек на скамейке по три.
Построим граф:
| К | Т | О | |||
| / | \ | / | \ | / | \ |
| Т | О | К | О | К | Т |
| | | | | | | | | | | | |
| О | Т | О | К | Т | К |
Девочки могут усесться на скамейке 6 способами: КТО, КОТ, ТКО, ТОК, ОКТ, ОТК.
2 способ. Эту задачу можно решить следующим способом: переставляя буквы К, Т, О (заглавные буквы имен девочек), получим упорядоченные тройки, у которых состав один и тот же, а вот порядок разный и, значит, число таких способов равняется P3=3!=6.
П р и м е р 10. Даны треугольники, квадраты и окружности. Сколько можно составить всевозможных пар фигур? При этом в расстановки могут входить и фигуры одного вида, а две расстановки считаются различными, если они отличаются друг от друга или составом входящих в них фигур, или порядком этих фигур.
Решение. Построим граф.
| ▲ | ■ | ● | ||||||
| / | | | \ | / | | | \ | / | | | \ |
| ■ | ▲ | ● | ■ | ▲ | ● | ■ | ▲ | ● |
Получим девять пар: ▲■, ▲▲, ▲●, ■▲, ■■, ■●, ●▲, ●■, ●●.
Упорядоченные наборы, в которых элементы могут повторяться (в отличие от множеств, где все элементы различны) называют кортежами. Наряду со словом «кортеж» применяют названия «размещение», «конечная последовательность», «вектор», «слово», «n –ками» (где n – число элементов в упорядоченном наборе).
В этой задаче мы вычисляли число кортежей длины 2, составленных из 3-элементного множества. Заметим, в этих соединениях важен как состав (выбор) элементов, так и порядок, причем элементы могут повторяться, следовательно, это размещение с повторением: 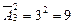 .
.
П р и м е р 11. На автоматической камере хранения – четыре диска с цифрами 0,1,…,9. Сколько секретных шифров можно составить?
Решение. Шифр на камере хранения это кортеж длины 4 из 10 цифр. Шифры с разным порядком цифр различаются, и цифры в шифре могут повторяться. Следовательно, число шифров – это число размещений с повторениями 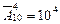 .
.
|
|
|
П р и м е р 12. Сколькими способами можно выбрать в кондитерской 3 пирожных, если имеется только 2 сорта их (например, «корзиночки» и «наполеоны»)?
Решение. Построим граф:
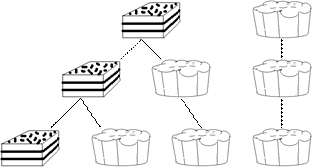
Таким образом, получились следующие наборы: ННН, ННК, НКК, ККК. Заметим, что в данном случае порядок не важен, наборы ННК и НКН одинаковы (пирожные одного вида не нумеруются, не различаются), а значит каждый набор пирожных (покупка) – это сочетание из 2 по 3 с повторениями
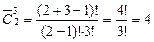
П р и м е р 13.Домино. На каждой костяшке домино по два числа от 0 до 6. Эти числа могут совпадать (дубли), а кости с разным порядком чисел (например, 2:3 и 3:2) не различаются. Определите число фишек (костей) в домино.
Решение. Обозначим все простые фишки (не дубли) правильными дробями: например, 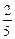 (а не
(а не 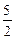 ). Значит нужно найти число правильных дробей со знаменателями не более шести и добавить к ним 7 дублей. Но число таких правильных дробей со знаменателями не более шести равно числу сочетаний из семи элементов (0,1,2,3,4,5,6) по 2, т.е.
). Значит нужно найти число правильных дробей со знаменателями не более шести и добавить к ним 7 дублей. Но число таких правильных дробей со знаменателями не более шести равно числу сочетаний из семи элементов (0,1,2,3,4,5,6) по 2, т.е. 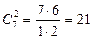 . Разных костей домино всего 21+7=28.
. Разных костей домино всего 21+7=28.
Такой же ответ мы получим, если заметим, что кости домино – это неупорядоченные выборки объема 2 из 7 чисел с повторениями. Число таких выборок составляет 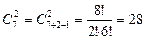 .
.
П р и м е р 14. Сколько «слов» можно получить, переставляя буквы в слове «АТАКА»?
Решение. В примере 8 мы поняли, что из пяти букв можно составить 5!=120 различных пятибуквенных «слов».
Но в слове «АТАКА» буква «А» встречается три раза и, следовательно, перестановка одинаковых букв (т.е. букв «А») не будет менять «слова». Поэтому общее число перестановок с повторениями во столько раз меньше числа перестановок без повторений, сколькими способами можно переставлять повторяющиеся буквы (элементы): в нашем случае было 5 элементов, из которых 3 повторяющиеся, то есть 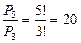 .
.
П р и м е р 15. Девочка получила 10 просверленных шариков из оргстекла: 5 белых, 2 красных и 3 голубых. Она продела в них нитку и надела как ожерелье на шею. Потом стала менять порядок расположения шариков, и каждый день ожерелье принимало другой вид. Сколько разных видов ожерелья может получить девочка?
Решение. Если бы шарики одного и того же цвета были различимы (пронумерованы или проиндексированы), то общее число разных расположений составило бы 10!=3628800 способов. Однако при любой перемене мест пяти белых шариков ожерелье не меняет своего вида, поэтому разных видов ожерелье будет меньше в 5!=120 раз. Те же соображения относятся и к двум красным и трем голубым шарикам. Значит, ожерелий будет 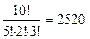 видов. Если еще учесть, что ожерелье замкнуто, т.е. последний шарик примыкает к первому, и циклическая перестановка шариков не меняет вида ожерелья, то окажется, что в действительности возможны только 252 различных вида.
видов. Если еще учесть, что ожерелье замкнуто, т.е. последний шарик примыкает к первому, и циклическая перестановка шариков не меняет вида ожерелья, то окажется, что в действительности возможны только 252 различных вида.
Для того чтобы безошибочно различать виды комбинаций (перестановки, размещения и сочетания), следует применять блок-схему «Комбинаторика» (рис.37)
Комбинаторные задачи не всегда рассчитаны на одну формулу. Обычно встречаются задачи на применение нескольких формул или правил комбинаторики.
П р и м е р 16. В мешке 25 шаров: 4 красных, 6 синих, 7 зеленых и 8 желтых. Сколькими способами можно достать 4 шара так, чтобы среди них были хотя бы три одинаковых?
Решение. «Хотя бы три» обозначает «ровно три» или «ровно четыре». Три красных шара можно выбрать из четырех имеющихся. Используем блок-схему «Комбинаторика» (см. рис.38): порядок расположения элементов значения не имеет, используются не все элементы (3 из 4) и элементы не повторяются. Следовательно, имеем дело с сочетаниями без повторений. Тогда число способов, которыми можно достать 3 красных шара из 4, равно 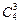 . При этом четвертый шар может быть синим, зеленым или желтым. Число способов, которыми можно его выбрать, по правилу суммы равно 6 + 7 + 8. Три красных шара в четверку можно выбрать
. При этом четвертый шар может быть синим, зеленым или желтым. Число способов, которыми можно его выбрать, по правилу суммы равно 6 + 7 + 8. Три красных шара в четверку можно выбрать 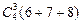 способами (по правилу произведения).
способами (по правилу произведения).
|

Рис.38
Таким образом, три одинаковых шара в четверку можно выбрать
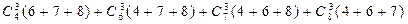 способами (по правилу суммы), а четыре одинаковых
способами (по правилу суммы), а четыре одинаковых 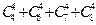 способами (по правилу суммы). Следовательно, общее число способов равно 2046 + 121 = 2167 (проверьте!).
способами (по правилу суммы). Следовательно, общее число способов равно 2046 + 121 = 2167 (проверьте!).
Так как комбинаторика является основной техникой, использующейся при решении вероятностных задач, рассмотрим следующие комбинаторные понятия и результаты.
Мы уже упоминали понятия выбор и выборка. Подчеркнем, что «выбор», как правило, означает сам процесс или факт совершения процесса выбирания. А «выборка» – это тот конкретный объект, который мы выбрали; выборка – это результат выбора.
Набор из k элементов n – множества называется выборкой объема k.
Если выборки, состоящие из одних и тех же элементов, но отличающиеся порядком их расположения, различаются, то это упорядоченные выборки; если же не различаются, то – неупорядоченные выборки.
Упорядоченные выборки объема k называются размещениями из n по k и обозначаются круглыми скобками (а1, а2,…, аk).
Неупорядоченные выборки объема k называются сочетаниями из n по k и обозначаются квадратными скобками [а1, а2,…, аk]. Понятно, что (1,2)≠(2,1), но [1,2]= [2,1].
Если элементы в выборке могут повторяться сколько угодно раз (т.е. извлеченный элемент возвращается и затем может появиться снова на другом месте), то такие выборки называются выборками с повторениями (или с возвращением). Если каждый элемент может встретиться в выборке только один раз, то такие выборки называются без повторений (или без возвращения). Таким образом, можно рассматривать, по крайней мере, четыре типа выборок: размещения с повторениями и без них и сочетания с повторениями и без них.
Вместо терминологии выборок иногда удобнее (нагляднее) использовать терминологию размещения шаров по ящикам. Каждой выборке 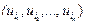 объема k из n элементов соответствует размещение k шаров по n ящикам, при этом первый шар помещают в ящик с номером i1,..., k -й шар – в ящик с номером ik. Упорядоченным выборкам соответствует случай, когда все шары различимы (например, пронумерованы), а неупорядоченным выборкам – случай, когда все шары неразличимы (одинаковы). Выборкам с повторениями соответствуют размещения без запрета, когда в каждый ящик помещается сколько угодно шаров, а выборкам без повторений – размещения с запретом, когда в один ящик помещается только один шар. Например, неупорядоченным выборкам [а, а] и [а, b] из совокупности U= {а, b, с} соответствуют следующие размещения двух одинаковых (одноцветных) шаров по трем ящикам: в первом случае оба шара помещают в первый ящик, а во втором – один шар кладут в первый ящик, другой – во второй. Упорядоченным выборкам соответствуют аналогичные размещения различных (разноцветных) шаров.
объема k из n элементов соответствует размещение k шаров по n ящикам, при этом первый шар помещают в ящик с номером i1,..., k -й шар – в ящик с номером ik. Упорядоченным выборкам соответствует случай, когда все шары различимы (например, пронумерованы), а неупорядоченным выборкам – случай, когда все шары неразличимы (одинаковы). Выборкам с повторениями соответствуют размещения без запрета, когда в каждый ящик помещается сколько угодно шаров, а выборкам без повторений – размещения с запретом, когда в один ящик помещается только один шар. Например, неупорядоченным выборкам [а, а] и [а, b] из совокупности U= {а, b, с} соответствуют следующие размещения двух одинаковых (одноцветных) шаров по трем ящикам: в первом случае оба шара помещают в первый ящик, а во втором – один шар кладут в первый ящик, другой – во второй. Упорядоченным выборкам соответствуют аналогичные размещения различных (разноцветных) шаров.
Таким образом, получаем: 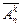 равно числу размещений k различимых шаров по n ящикам без запрета;
равно числу размещений k различимых шаров по n ящикам без запрета;
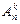 равно числу размещений k различимых шаров по n ящикам с запретом;
равно числу размещений k различимых шаров по n ящикам с запретом;
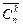 равно числу размещений k неразличимых шаров по n ящикам без запрета;
равно числу размещений k неразличимых шаров по n ящикам без запрета;
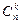 равно числу размещений k неразличимых шаров по n ящикам с запретом.
равно числу размещений k неразличимых шаров по n ящикам с запретом.
Формулы для вычисления 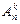 ,
, 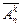 ,
, 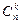 ,
, 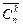 проиллюстрированы на рис. 39 на примере выборок объема k = 2 из совокупности U= {а, b, с} и соответствующих им размещений двух шаров по трем ящикам.
проиллюстрированы на рис. 39 на примере выборок объема k = 2 из совокупности U= {а, b, с} и соответствующих им размещений двух шаров по трем ящикам.
| Упорядоченные (размещения) | Неупорядоченные (сочетания) | ||||||||||||||||||||||||||
| С возвращением | Без запрета | ||||||||||||||||||||||||||
| ● | ○ | ||||||||||||||||||||||||||
| ○ | ○ | ● | ○ | ● | ○ | ○ | ○ | ○ | ○ | ||||||||||||||||||
| (а, а) | (а, b) | (а, c) | [а, а] | [а, b] | [а, c] | ||||||||||||||||||||||
| ● | ○ | ||||||||||||||||||||||||||
| ● | ○ | ○ | ○ | ● | ○ | ○ | ○ | ||||||||||||||||||||
| (b, a) | (b, b) | (b, c) | [b, b] | [b, c] | |||||||||||||||||||||||
| ● | ○ | ||||||||||||||||||||||||||
| ● | ○ | ● | ○ | ○ | ○ | ||||||||||||||||||||||
| (c, a) | (c, b) | (c, c) | [c, c] | ||||||||||||||||||||||||
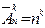 | 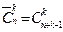 | ||||||||||||||||||||||||||
| Без возвращения | С запретом | ||||||||||||||||||||||||||
| ○ | ● | ○ | ● | ○ | ○ | ○ | ○ | ||||||||||||||||||||
| (а, b) | (а, c) | [а, b] | [а, c] | ||||||||||||||||||||||||
| ● | ○ | ○ | ● | ○ | ○ | ||||||||||||||||||||||
| (b, a) | (b, c) | [b, c] | |||||||||||||||||||||||||
| ● | ○ | ● | ○ | ||||||||||||||||||||||||
| (c, a) | (c, b) | ||||||||||||||||||||||||||
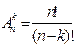 | 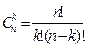 | ||||||||||||||||||||||||||
| Различимые шары | Неразличимые шары |
Рис.39
 2015-05-13
2015-05-13 3629
3629








