1. Известно, что 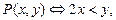
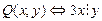 .Найти значение истинности следующих высказываний:
.Найти значение истинности следующих высказываний:
а) 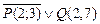 ; б)
; б) 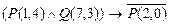 ;
;
в) 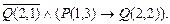
2. Известно, что предикаты 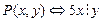 и
и 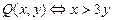 имеют натуральные предметные переменные. Построить начала их таблиц истинности и выяснить истинностные значения следующих высказываний:
имеют натуральные предметные переменные. Построить начала их таблиц истинности и выяснить истинностные значения следующих высказываний:
а) 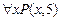 ; б)
; б) 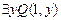 ; в)
; в) 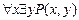 .
.
3. Пусть предикаты 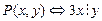 и
и 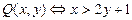 определены на множестве натуральных чисел. Зададим новые Z предикаты
определены на множестве натуральных чисел. Зададим новые Z предикаты 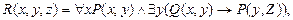
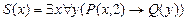 . Найти истинностные значения следующих высказываний:
. Найти истинностные значения следующих высказываний:
а) 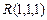 ; б)
; б) 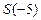 ; в)
; в) 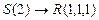 .
.
4. Записать формулой алгебры предикатов следующие предложения:
а) «если х простое число, то оно не делится ни на какое простое у»;
б) «если число х делится на 2 и на 3, то оно составное»;
в) «каждый квадрат являются параллелограммом»;
е) «каждое простое число нечетно, но существуют нечетные составные числа».
5. Зная, что 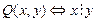 и
и 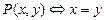 следующие формулы предикатов алгебры сформулировать по-русски:
следующие формулы предикатов алгебры сформулировать по-русски:
а) 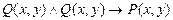 ;
;
б) 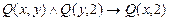 ;
;
в) 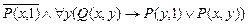 .
.
6. На графике изобразить области истинности предикатов с действительными предметными переменными:
а) 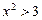 ; б)
; б) 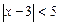 ; в)
; в) 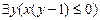 ;
;
г) 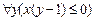 ; д)
; д) 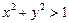 .
.
7. Пусть 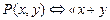 – четное число»,
– четное число», 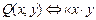 – четное число» определены на Z. Найти истинностные значения высказываний:
– четное число» определены на Z. Найти истинностные значения высказываний:
а) 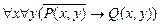 ;
;
б) 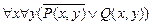 ;
;
в) 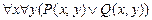 .
.
8. Проверить, имеет ли место логическое следование, если все участвующие в записях предметные переменные являются действительными:
а) 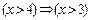 ; б)
; б) 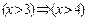 ; в)
; в) 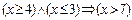 .
.
9. С помощью равносильностей алгебры предикатов доказать: а) 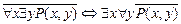 ;
;
б) 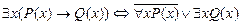 ;
;
в) 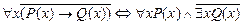 .
.
10. Для следующих утверждений сформулировать обратное, противоположное, обратное противоположному и выяснить, какие из них являются теоремами:
а) «Если в четырехугольник можно вписать окружность, то этот четырехугольник является ромбом»;
б) «Если четырехугольник является ромбом, то его диагонали взаимно перпендикулярны»;
в) «Если два числа делятся на 7, то их произведение делится на 7».
11. Следующие формулы алгебры предикатов записать с ограниченными кванторами: а) 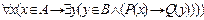 ;
;
б) 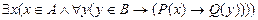 .
.
12. Следующие формулы с ограниченными кванторами записать с обычными кванторами: а) 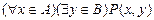 ;
;
б) 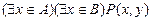 .
.
13. Перевести предложение на логический язык, построить его отрицание и полученное отрицание перевести на русский язык:
а) «Для любых натуральных чисел х и у существует натуральное число 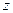 такое, что если
такое, что если 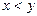 », то
», то 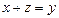 »;
»;
б) «Для любых натуральных чисел х и у и 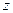 , если
, если 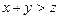 и
и 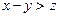 , то
, то 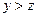 »;
»;
в) «Существует натуральное число у такое, что если 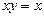 », то для любого натурального числа
», то для любого натурального числа 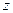 верно
верно 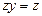 ».
».
14. Найти области истинности предикатов, определенных на множестве действительных чисел:
а) 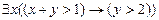 ; б)
; б) 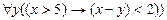 ;
;
в) 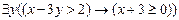 ; г)
; г) 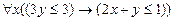 .
.
15. Перевести предложение на логический язык, построить его отрицание и это отрицание перевести на русский язык:
а) «Если при всяком положительном х разность  положительна, то у отрицателен»;
положительна, то у отрицателен»;
б) «Если при некотором отрицательном х произведение ху отрицательно, то у положителен»;
в) «Если существует неотрицательное х такое, что разность 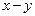 отрицательна, то у отрицателен», то для любого натурального числа
отрицательна, то у отрицателен», то для любого натурального числа 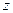 верно
верно 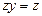 »;
»;
г) «Если при некотором у произведение 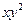 положительно, то х положителен»;
положительно, то х положителен»;
д) «Если при всяком положительном х сумма 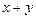 больше единицы, то у положителен».
больше единицы, то у положителен».
16. Если 6 – составное число (A), то 12 – составное число (B). Если 12 – составное число, то существует простое число больше чем 12 (C). Если существует простое число больше 12, то существует составное число больше 12 (D). Если 6 делится на 2 (E), то 6 – составное число. Число 12 составное. Следует ли отсюда, что 6 – составное число?
17. Если я поеду автобусом (А), а автобус опоздает (В), то я пропущу назначенное свидание (С). Если я пропущу назначенное свидание и начну огорчаться (D), то мне не следует ехать домой (E). Если я не получу работу (Р), то я начну огорчаться и мне следует поехать домой. Следует ли тогда, что если я поеду автобусом и автобус опоздает, то я получу работу?
18. Если Сергей выиграет теннисный турнир (А), то он будет доволен (В), а если он будет доволен, то он плохой борец в последующих турнирах (С). Но если он проиграет этот турнир, то потеряет поддержку своих болельщиков (D). Он плохой борец в последующих турнирах, если потеряет поддержку своих болельщиков. Если он плохой борец в последующих турнирах, то ему следует прекратить занятия теннисом (E). Сергей или выиграет этот турнир, или проиграет его. Следовательно, ему нужно прекратить занятия теннисом. Справедливо ли приведенное рассуждение с точки зрения логики?
19. Или Анна и Антон одного возраста (А), или Анна старше Антона (В). Если Анна и Антон одного возраста, то Наташа и Антон не одного возраста (С). Если Анна старше Антона, то Антон старше Николая (D). Следует ли отсюда, что либо Наташа и Антон не одного возраста, либо Антон старше Николая?
20. Для предложения: «Если каждое слагаемое суммы четно, то сумма четна» сформулируйте обратное, противоположное и обратно-противоположное предложения. Какие из них верны?
21. Сформулируйте теорему «Если два прямоугольника равны, то площади их равны» в виде:
а) необходимого условия; б) достаточного условия.
22. Утверждение «Равенство треугольников есть достаточное условие их равновеликости» сформулируйте в виде условного предложения (в форме «если А, то В»).
23. Утверждение «Четность суммы есть необходимое условие четности каждого слагаемого» сформулируйте в виде условного предложения.
24. Утверждение «Для того чтобы диагонали четырехугольника были перпендикулярны, достаточно, чтобы этот четырехугольник был ромбом» сформулируйте в виде: а) условного предложения; б) необходимого условия.
25. Теорему «Параллелограмм является ромбом тогда и только тогда, когда его диагонали взаимно перпендикулярны» сформулируйте в виде необходимого и достаточного условия (дайте две формулировки).
26. Родители сказали детям: «Если мы поедем в дом отдыха, то вы поедете в лагерь». В школе детей спросили, куда они поедут летом. «Если мы поедем в лагерь, то родители поедут в дом отдыха», – ответил Петя. Галя сказала: «Если папа с мамой не поедут в дом отдыха, то мы не поедем в лагерь». «Нет, не так, – вмешался Коля. – Если мы не поедем в лагерь, то родители не поедут в дом отдыха». Чей ответ равносилен тому, что сказали родители? Кто из детей сказал разными словами одно и то же?
27. Докажите, что для любого натурального n справедливо равенство:
а) 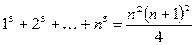 ;
;
б) 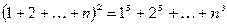 ;
;
в) 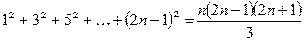 ;
;
г) 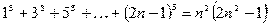 ;
;
д) 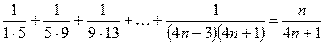 ;
;
е)  .
.
28. Пусть 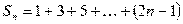 . Найдите выражение для
. Найдите выражение для 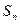 , докажите.
, докажите.
29. При каких 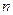 справедливо неравенство
справедливо неравенство 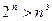 ?
?
30. При каких 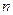 справедливо неравенство
справедливо неравенство 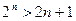 ?
?
31. Докажите, что 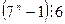 .
.
32. Докажите, что 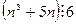 .
.
33. Доказать, что 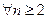
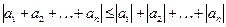
34. Пусть 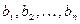 – геометрическая прогрессия со знаменателем
– геометрическая прогрессия со знаменателем 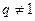 . Докажите, что
. Докажите, что 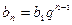 ,
, 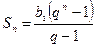 .
.
35. Докажите неравенство Бернулли для любого действительного 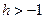 :
: 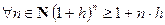 .
.
36. Докажите, что 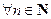
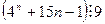
37. Докажите, что 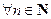
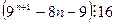 .
.
38. Докажите, что 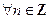
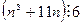 .
.
39. Докажите, что сумма кубов трех последовательных натуральных чисел делится на 9.
40. Докажите, что 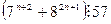
41. Докажите, что при целом четном 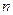
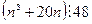 .
.
42. Докажите, что 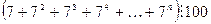 при любом натуральном
при любом натуральном 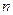 , кратном 4.
, кратном 4.
43. Докажите, что число, запись которого состоит из 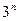 единиц, делится на
единиц, делится на 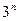 .
.
44. Пусть 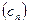 – последовательность:
– последовательность: 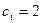 ,
, 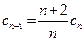 . Докажите, что
. Докажите, что 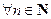
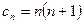 .
.
45. Пусть 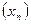 – последовательность,
– последовательность, 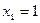 ,
, 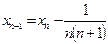 . Найдите выражение
. Найдите выражение 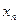 через
через 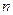 , доказать его справедливость при всех натуральных
, доказать его справедливость при всех натуральных 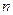 .
.
46. Пусть 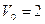 ,
, 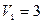 ,
,  . Докажите, что
. Докажите, что 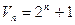 для всех
для всех 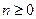 .
.
47. Пусть 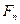 – последовательность Фибоначчи:
– последовательность Фибоначчи: 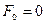 ,
, 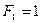 ,
, 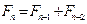 . Докажите, что
. Докажите, что 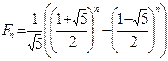 .
.
48. Докажите свойства чисел Фибоначчи:
1) 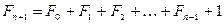 ;
;
2) 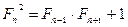 (рассмотреть отдельно четные, нечетные номера).
(рассмотреть отдельно четные, нечетные номера).
49. Пусть 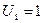 ,
, 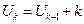 . Докажите, что
. Докажите, что 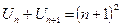 .
.
50. Пусть 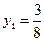 ,
, 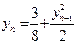 . Докажите, что
. Докажите, что 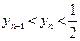 .
.
51. Докажите, что 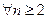
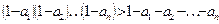 при
при 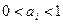 ,
, 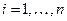 .
.
52. Пусть 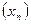 – последовательность,
– последовательность, 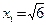 ,
, 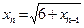 . Докажите, что
. Докажите, что 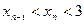 .
.
53. Докажите, что 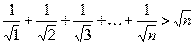 при
при 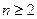 .
.
54. Докажите, что 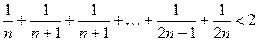
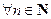 .
.
55. Докажите, что 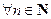
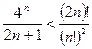 .
.
56. Докажите, что 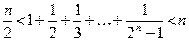 при
при 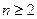 .
.
57. Докажите 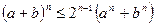 при
при 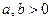 .
.
58. Докажите, что среднее геометрическое положительных чисел не больше их среднего арифметического: 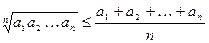 .
.
 2015-05-13
2015-05-13 1897
1897








