Модель сезонного роста

Дифференциальное уравнение первого порядка 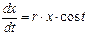, где r – положительная постоянная, можно рассматривать как модель сезонного роста. Скорость роста 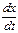популяции 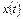становится попеременно то положительной, то отрицательной и численность популяции то возрастает то убывает.

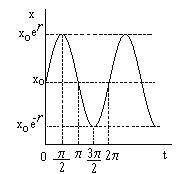
Это может вызываться такими сезонными факторами, как доступность пищи. Общее решение записывается так: 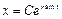; t=0 С=x₀, т. е. размер популяции в момент t есть 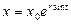. Максимальный размер популяции, равный 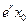, достигается при 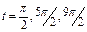, когда sin(t)=1. Минимальный размер, равный 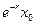достигается при 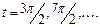,когда 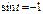. В этой модели размер популяции колеблется от 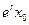до 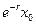с периодом в 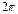. Моменты времени 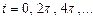можно считать серединами сезонов наибольшей доступности пищи (летних сезонов), а 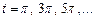,соответствует серединам сезонов наибольшей нехватки пищи (зимних сезонов). Продолжительность 1 года соответствует 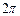единицам времени.