Качественные методы исследования подобных систем рассмотрим на моделях, представимых в виде систем двух автономных дифференциальных уравнений:
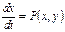
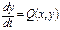
Здесь 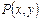 ,
, 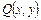 - непрерывные функции, определенные в некоторой евклидовой плоскости (x,y – декартовы координаты) и имеющие в этой области непрерывные производные порядка не ниже первого.
- непрерывные функции, определенные в некоторой евклидовой плоскости (x,y – декартовы координаты) и имеющие в этой области непрерывные производные порядка не ниже первого.
Область может быть как неограниченной, так и ограниченной. В том случае, когда переменные величины 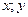 имеют конкретный биологический смысл, на них накладываются некоторые ограничения. Прежде всего, биологические переменные не могут быть отрицательными. Так, в модели Вольтерра,
имеют конкретный биологический смысл, на них накладываются некоторые ограничения. Прежде всего, биологические переменные не могут быть отрицательными. Так, в модели Вольтерра, 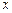 - переменная, характеризующая численность жертвы, а
- переменная, характеризующая численность жертвы, а 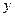 - хищника. Область
- хищника. Область 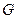 представляет собой положительный квадрат правой полуплоскости:
представляет собой положительный квадрат правой полуплоскости:
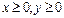
В процессе изменения состояния системы во времени переменные 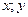 изменяются согласно системе уравнений, так что каждому состоянию системы соответствует пара значений
изменяются согласно системе уравнений, так что каждому состоянию системы соответствует пара значений 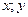 . Рассмотрим плоскость с осями координат, на которых отложены значения переменных
. Рассмотрим плоскость с осями координат, на которых отложены значения переменных 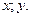 Такая плоскость носит название фазовой плоскости. Она представляет совокупность всех возможных состояний системы.
Такая плоскость носит название фазовой плоскости. Она представляет совокупность всех возможных состояний системы.
Точка 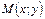 называется изображающей. Пусть, при
называется изображающей. Пусть, при 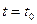 , координаты изображающей точки
, координаты изображающей точки 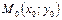 . В каждый следующий момент времени
. В каждый следующий момент времени 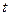 изображающая точка будет двигаться в соответствии с системой уравнений и принимать положение
изображающая точка будет двигаться в соответствии с системой уравнений и принимать положение 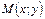 , соответствующее значениям
, соответствующее значениям 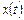 ,
, 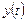 .
.
Совокупность этих точек на фазовой плоскости 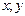 называется фазовой траекторией. Характер фазовых траекторий отражает общие качественные черты поведения системы во времени.
называется фазовой траекторией. Характер фазовых траекторий отражает общие качественные черты поведения системы во времени.
Изображающая точка с координатами 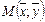 , называется стационарной, и в этой точке
, называется стационарной, и в этой точке
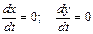
 2015-05-13
2015-05-13 957
957








