Разновидностью модели раздельного течения является модель потока дрейфа. Она отличается от описанной выше модели раздельного течения тем, что рассматривается только относительное движение фаз. Модель потока дрейфа используется при исследовании потоков газожидкостных смесей и взвесей твёрдых частиц в жидкости или газе. Свойства таких систем часто определяются не относительными расходами фаз, а размерами частиц дисперсной фазы и их объёмным содержанием.
 Метод расчёта параметров движения двухфазного потока основывается на определении приведённой скорости дрейфа
Метод расчёта параметров движения двухфазного потока основывается на определении приведённой скорости дрейфа 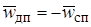 - см. выражение (13.12). Эта величина равна разности скорости движения каждого компонента и средней скорости смеси. Поскольку приведённые скорости движения фаз, согласно (13.4), зависят лишь от их расхода и площади поперечного сечения канала, то приведённая скорость дрейфа в соответствии с (13.13) является функцией только объёмной концентрации дисперсной фазы j и свойств системы. Если скорости движения сплошной и дисперсной фаз одинаковы (это возможно при одинаковых плотностях фаз или при очень малых размерах частик как, например, в аэрозолях), то приведённая скорость дрейфа равна нулю. Это вытекает из определения (13.9) и выражения (13.14). Из (13.14) следует, что
- см. выражение (13.12). Эта величина равна разности скорости движения каждого компонента и средней скорости смеси. Поскольку приведённые скорости движения фаз, согласно (13.4), зависят лишь от их расхода и площади поперечного сечения канала, то приведённая скорость дрейфа в соответствии с (13.13) является функцией только объёмной концентрации дисперсной фазы j и свойств системы. Если скорости движения сплошной и дисперсной фаз одинаковы (это возможно при одинаковых плотностях фаз или при очень малых размерах частик как, например, в аэрозолях), то приведённая скорость дрейфа равна нулю. Это вытекает из определения (13.9) и выражения (13.14). Из (13.14) следует, что 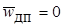 при j = 0 и j = 1. Таким образом, если плотности фаз различны, то
при j = 0 и j = 1. Таким образом, если плотности фаз различны, то 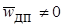 и зависимость
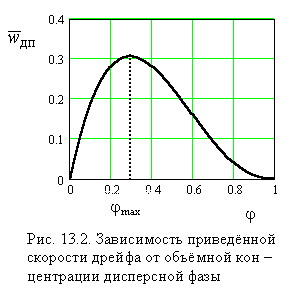
и зависимость 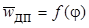 изображается кривой, характерный вид которой показан на рис. 13.2 для системы, в которой скорость движения дисперсной фазы больше скорости сплошной фазы. При значении jmax частицы дисперсной фазы приходят в соприкосновение, и дальнейшее увеличение j обусловливает уменьшение приведённой скорости дрейфа. Значение jmax зависит от формы и размеров частиц, а также от характера сил взаимодействия между ними. Точка jmax соответствует обращению системы. При j > jmax дисперсная фаза становится сплошной, а сплошная – дисперсной. Очевидно, такое обращение фаз возможно, если они обе они подвижны. Для систем жидкость – твёрдые частицы область j > jmax не имеет физического смысла.
изображается кривой, характерный вид которой показан на рис. 13.2 для системы, в которой скорость движения дисперсной фазы больше скорости сплошной фазы. При значении jmax частицы дисперсной фазы приходят в соприкосновение, и дальнейшее увеличение j обусловливает уменьшение приведённой скорости дрейфа. Значение jmax зависит от формы и размеров частиц, а также от характера сил взаимодействия между ними. Точка jmax соответствует обращению системы. При j > jmax дисперсная фаза становится сплошной, а сплошная – дисперсной. Очевидно, такое обращение фаз возможно, если они обе они подвижны. Для систем жидкость – твёрдые частицы область j > jmax не имеет физического смысла.
Зависимость 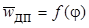 определяется по опытным данным. Типичное корреляционное уравнение, описывающее эту зависимость, имеет вид:
определяется по опытным данным. Типичное корреляционное уравнение, описывающее эту зависимость, имеет вид:
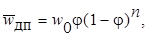 (13.40)
(13.40)
где w 0 – скорость движения одиночной частицы в бесконечном объёме сплошной фазы; n – коэффициент, являющийся функцией числа Рейнольдса.
Величина w 0 определяется из условия равенства сил тяжести и сопротивления сплошной фазы, действующих на частицу. Для сферической частицы это условие выражается равенством
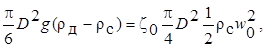 (13.41)
(13.41)
где D – диаметр частицы; z0 – коэффициент сопротивления, зависящий от числа Рейнольдса Re0 = rc w 0 D /hc – см. рис. 13.3.
Уравнение (13.41) можно представить в безразмерной форме. Выражая скорость через число Рейнольдса и преобразуя правую часть, получаем:
z0Re02 =
= 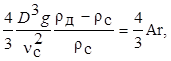 (13.42)
(13.42)
где Ar – число Архимеда
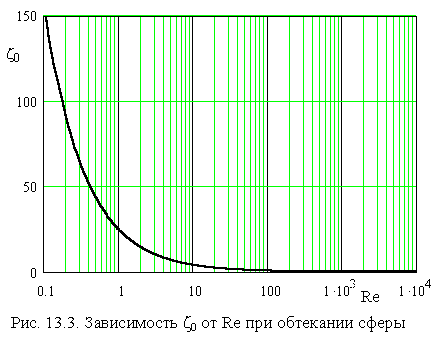 Ar = (D 3 g /nc2)×(rд - rс)/rс.
Ar = (D 3 g /nc2)×(rд - rс)/rс.
Таким образом, величина z0Re0 не зависит от w 0, а является функцией только физико-механических свойств системы. В большинстве практически важных случаях для системы жидкость – твёрдые частицы Re0 < 500. При этом зависимость z0 от Re0 можно представить формулой
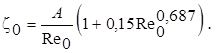 (13.43)
(13.43)
Для сферической частицы А = 24. При Re0 > 500
z0 = 0,44. (13.44)
С помощью приведённых зависимостей находится значение w 0.
На основании опытных данных предложены следующие зависимости для определения n в формуле (13.40):
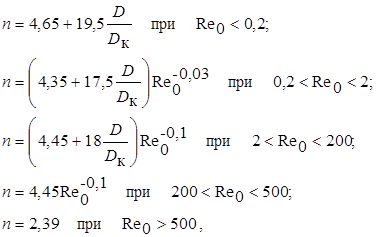 (13.45)
(13.45)
где D – диаметр частицы; D к – диаметр канала, в котором движутся частицы.
Для частиц, форма которых отличается от сферической, в качестве определяющего размера принимается эквивалентный диаметр, равный диаметру сферы того же объёма V, что и рассматриваемая частица:
V = p D э3/6 или D э = 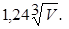
Движущиеся в вязкой жидкости частицы несферической формы уже при малых значениях числа Рейнольдса (³ 0,05) ориентируются наибольшей площадью проекции вдоль потока жидкости. Для частиц, имеющих форму тетраэдра и куба, такое ориентирование полностью устанавливается при Re = 10, а для частиц иной формы – при Re = 20. При значениях Re = = 70 ¸ 300 возникает нестабильность движения частиц, проявляющаяся в колебаниях и вращении.
Влияние формы частицы на коэффициент сопротивления z0 учитывается с помощью так называемого фактора (или коэффициента) формы y, определяемого как отношение поверхностей сферической F с и рассматриваемой F частиц одинакового объёма:
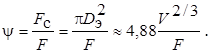

Для несферических частиц коэффициент сопротивления при Re0 < 500 определяется по формуле (13.43), в которой, согласно опытным данным,
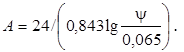
При Re0 > 500 значение z0 находится с помощью эмпирического соотношения z0 = 5,32 – 4,88 y. Для сферических частиц y = 1, для несферических y < 1. Чем меньше y, тем больше z0 и меньше, согласно равенству (13.41), скорость движения частицы (скорость осаждения) w 0.
При одновременном движении большого числа частиц вместо z0 в уравнении (13.42) нужно использовать коэффициент сопротивления z, который можно представить в виде произведения z0 для одиночной частицы на функцию концентрации частиц f (j), учитывающую особенности их группового движения
z = z0 f (j). (13.46)
Величина z0 представляет собой коэффициент сопротивления одиночной частицы, движущейся в неподвижной жидкости с той же относительной скоростью w дп, что и в рассматриваемом потоке. Согласно (13.11) и (13.12), 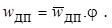 Поэтому из (13.40) следует:
Поэтому из (13.40) следует:
w дп = w 0(1 - j) n. (13.47)
Коэффициент z0 рассчитывается по приведённым выше зависимостям, в которых число Рейнольдса определяется выражением:
Reд = rс w дп D э/hс.
Функция f (j) находится следующим образом.
В состоянии равновесия значения zRe2 для частицы определённого размера одинаковы независимо от того, является она одиночной или нет Поэтому
zReд2 = z0Re02 = (4/3)Ar. (13.48)
Отсюда с учётом (13.43), (13.44) и (13.46) получаем при Re < 500
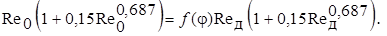 (13.49)
(13.49)
При Re > 500
Re02 = f (j)Reд2. (13.50)
Умножая левую и правую части выражения (13.47) на rс D с/hс, получим
Reд = Re0(1 - j) n.
При сопоставлении последнего равенства с выражением (13.50) нетрудно установить, что при Re > 500 величина f (j) = (1 - j)- 2 n. Сопоставляя то же равенство с уравнением (13.49) получаем при низких значениях числа Рейнольдса, т.е. когда величина 0,15Re0,687 мала по сравнению с единицей f (j) = (1 - j)- n.
Учитывая выражения (13.45), приходим к выводу, что величина f (j) изменяется в следующих пределах: f (j) = (1 - j)- 4,78 ¸ (1 - j)- 4,65. Поэтому можно принять
f (j) = (1 - j)- 4,7. (13.51)
Поскольку (1 - j) £ 1, то f (j) ³ 1, и коэффициент сопротивления z при групповом движении частиц, согласно формуле (13.46), больше, чем для одиночной частицы. В соответствии с уравнениями (13.48) отсюда следует, что скорость движения частиц относительно сплошной среды уменьшается с увеличением их концентрации.
Выше рассмотрены лишь общие закономерности и модели, используемые для описания движения двухфазных сред. При описании закономерностей дросселирования потоков, их движения в трубах и каналах с поворотами, в трубах Вентури и т.п. приходится применять большое количество экспериментальных зависимостей (корреляций) и дополнительных методик расчёта. Со многими из них можно ознакомиться по монографии Д. Чисхолм "Двухфазные течения в трубопроводах и теплообменниках". – М.: Недра, 1986. – 204 с.
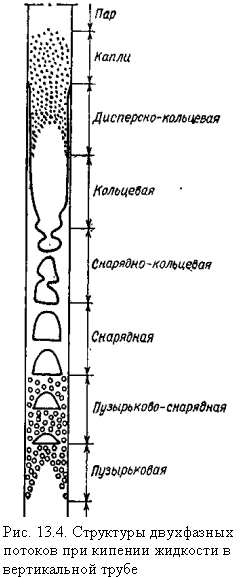 Ниже в качестве примера конкретизации приведённых выше зависимостей рассмотрены вопросы анализа закономерностей развития двухфазных потоков в системах жидкость – газ. Параметры движение газа в плотном движущемся слое описаны в гл.8 и гл.12, а расчёт течений в системах газ – твёрдое тело составляет теоретические основы механики аэрозолей (см., например, учебник Швыдкий В.С., Ладыгичев М.Г., Швыдкий Д.В. Теоретические основы очистки газов. - М.: Машиностроение, 2001. – 502 с.).
Ниже в качестве примера конкретизации приведённых выше зависимостей рассмотрены вопросы анализа закономерностей развития двухфазных потоков в системах жидкость – газ. Параметры движение газа в плотном движущемся слое описаны в гл.8 и гл.12, а расчёт течений в системах газ – твёрдое тело составляет теоретические основы механики аэрозолей (см., например, учебник Швыдкий В.С., Ладыгичев М.Г., Швыдкий Д.В. Теоретические основы очистки газов. - М.: Машиностроение, 2001. – 502 с.).
 2015-05-13
2015-05-13 2056
2056








