Пример выполнения задания Д4

Механическая система с двумя степенями свободы, состоящая из четырех абсолютно твердых тел, соединенных между собой нерастяжимыми невесомыми нитями (груз 3 подвешен к блоку 1 с неподвижной осью, а груз 4 подвешен к блоку 2 с подвижной осью), приходит в движение из состояния покоя под действием сил тяжести. Груз 3 подвешен на пружине жесткостью с. Пренебрегая потерями на трение и считая, что в начальный момент времени груз, подвешенный на пружине, находился в положении статического равновесия, составить с помощью уравнений Лагранжа дифференциальные уравнения движения механической системы и определить закон относительного движения груза, подвешенного на пружине, а также частоту, период и амплитуду относительных колебаний груза.

Дано: m₁ = 4 кг, m₂ = 2 кг, m₃ = 10 кг, m₄ = 20 кг, R₁ = 40 см, r₁ = 20 см, r₁ = 30 см, R₂ = 10 см, с = 20 кН/м.

Определить: x = f(t) - закон относительного движения груза, подвешенного на пружине, а также частоту, период и амплитуду относительных колебаний груза.

Решение.

P₁

ds₃

P₃ C ds_Cdj

P₂ j

F_упр2

F_упр4

ds₄x

dx

P₄

Рис. 4.1.

Для системы с двумя степенями свободы выберем две обобщенные координаты: q₁ = x – относительное перемещение груза 4, равное деформации пружины, и q₂ = j - угол поворота тела 2. Запишем уравнения Лагранжа:

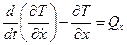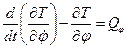; (4.1)

Определим кинетическую энергию системы:

T =T₁+T₂+T₃+T₄ (4.2)

Найдем кинетическую энергию каждого тела, учитывая, вращательное движение блока 1, плоско-параллельное движение блока 2 и поступательные движения грузов 3 и 4:

T₁ = 0,5 I₁w₁²; T₂ = 0,5(m₂V_C² + I_Cw₂²); T₃ = 0,5 m₃V₃²; T₄ = 0,5 m₄V₄² (4.3)

где I₁ = m₁r₁² – момент инерции блока 1 относительно его оси вращения, I_С = 0,5 m₂R₂² – момент инерции блока 2, представляющего собой сплошной однородный цилиндр, относительно оси, проходящей через его центр масс.

Выразим все скорости через обобщенные скорост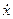и и 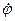. Очевидно, что

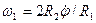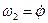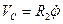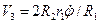, , , . (4.4)

Для определения скорости груза 4 рассмотрим его движение как сложное. Абсолютная скорость тела 4 равна алгебраической сумме переносной скорости точки С и относительной скорости груза, равной скорости удлинения пружины:

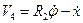(4.5)

Подставим все найденные выражения в формулу (4.2) и получим:

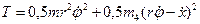, (4.6)

где для краткости принято r = R2, m = 4(m₁r₁²+m₃r₁²)/R₁²+1,5m₂ (4.7)

Изобразим на рис. 4.1 действующие на систему активные силы: силы тяжести P₁, P₂, P₃, P₄ и силы упругости F_упр4 и F_упр2, модули которых равны:

P₁ = m₁g; P₂ = m₂g; P₃ = m₃g; P₄ = m₄g;F_упр4 = F_упр2= cx (4.8)

Для определения обобщенной силы Q_x сообщим системе возможное перемещение, при котором обобщенная координата x получит положительное приращение dx, а j останется неизменной, то есть dj = 0 (переместится на расстояние dx только груз 4, а остальные тела останутся в покое). Тогда элементарную работу совершат только силы P₄ и F_упр4:

dA_x = P₄dx - F_упр4dx = (P₄dx - F_упр4)dx (4.9)

Для определения обобщенной силы Q_j сообщим системе возможное перемещение, при котором обобщенная координата j получит положительное приращение dj, а x останется неизменной, то есть dx = 0 (пружина при таком перемещении системы не изменяет свою длину). Тогда элементарную работу совершат только силы P₂, P₃ и P₄:

dA_x = P₃ds₃ – P₂ds_c - P₄ds₄ = (2P₃r₁R₂/R₁-P₂R₂-P₄R₂)dj (4.10)

При выводе уравнения (4.10) использовались уравнения (4.4), так как соотношения между перемещениями аналогичны соотношениям между соответствующими скоростями, при этом учтено, что ds_c= ds₄ (пружина не изменяет свою длину).

Коэффициенты перед приращениями dx и dj в уравнениях (4.9) и (4.10) и будут обобщенными силами Q_x, и Q_j,которые запишем с учетом (4.8):

Q_x = m₄g –cx; Q_j = m_jrg (4.11)

где для краткости принято r = R₂, m_j = 2m₃r₁/R₁- m₂ – m₄ (4.12)

Подставляя величины (4.6) и (4.11) в уравнения (4.1),получим следующие дифференциальные уравнения движения системы:

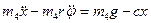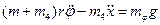; (4.13)

Для определения x = f(t) исключим из уравнений (4.13) 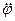и получим дифференциальное уравнение вида:

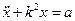, (4.14)

где k²=c(1/m₄+1/m); a =g(m+m₄ +m_j)/m (4.15)

Общее решение уравнения (4.14), как известно из курса высшей математики, имеет вид x = x_общ+ x_част , где x_общ – общее решение однородного уравнения

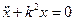, то есть x_общ = C₁sin(kt)+ C₂cos(kt), а x_част – частное решение уравнения (4.14). Будем искать решение в виде x_общ = В = const. Подставляя значение x_общ = В в (4.14), получим В =a/k². Таким образом общее решение уравнения (8.14) имеет вид:

x = C₁sin(kt)+ C₂cos(kt)+ a/k², (4.16)

где С₁ и С₂ – постоянные интегрирования, для определения которых найдем еще производную по времени от x:

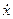= C₁k cos(kt) - C₂k sin(kt), (4.17)

Поскольку система начинает движение из состояния покоя с недеформированной пружиной, начальные значения переменных равны нулю, то есть при t = 0 x = 0 и 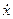= 0. Подставляя эти величины в уравнения (4.16) и (4.17), найдем постоянные интегрирования: С₁ =0 и С₂= - a/k².

Подставив полученные значения постоянных интегрирования в уравнение (8.16), окончательно получим искомое уравнение относительного движения груза 4:

x = a/k²(1-cos(kt)). (4.18)

Таким образом груз 4 совершает по отношению к точке C подвеса пружины гармонические колебания по закону (4.18) с амплитудой А = a/k²= 0,00712 м, ч астотой k =43,7 с^-1 и периодом T=2p/k = 0,144 c.