Механическая система с одной степенью свободы, состоящая из четырех абсолютно твердых тел, соединенных между собой нерастяжимыми невесомыми нитями (груз 3 подвешен к блоку 1 с неподвижной осью, а груз 4 подвешен к блоку 2 с подвижной осью), приходит в движение из состояния покоя под действием сил тяжести. Считая связи идеальными, определить с помощью общего уравнения динамики ускорение одного из тел механической системы или ускорение оси (центра масс) блока 2 (в зависимости от варианта).
Для сдвоенных блоков заданы большой и малый радиусы R и r и радиус инерции r. Массу одинарных блоков считать равномерно распределенной по ободу с радиусом R. Величины, отсутствующие в варианте из таблицы не выписывать: например, для варианта 2 игнорировать значения r1, r1 (тело 1 представляет собой однородный цилиндр радиуса R1).
Таблица Д3.1. Варианты задания Д3.
| Величина | Вариант | ||||||
| Обозначение | Измерение | ||||||
| m1 | кг | ||||||
| m2 | кг | ||||||
| m3 | кг | ||||||
| m4 | кг | ||||||
| R1 | см | ||||||
| r1 | см | ||||||
| r1 | см | ||||||
| R2 | см | ||||||
| r2 | см | ||||||
| r2 | см | ||||||
| Определить | e1 | e2 | a 3 | a 4 | a c | e1 |
Таблица Д3.2. Рисунки к заданию Д3.
                                                         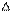                  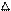 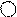                    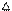                           1 1
| |||||
                                                                                                                          7 7
| |||||
                                                                                                                         13 13
| |||||
                                                                                                                        19 19
|   24 24
| ||||
                                                                                                                             25 25
|
 2015-05-13
2015-05-13 572
572








