1) Числовой ряд. Необходимый признак сходимости.
Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).
Рассматриваются числовые ряды двух видов
- вещественные числовые ряды — изучаются в математическом анализе;
- комплексные числовые ряды — изучаются в комплексном анализе;
Важнейший вопрос исследования числовых рядов — это сходимость числовых рядов. Числовые ряды применяются в качестве системы приближений к числам.
Числовой (действительный или комплексный) ряд 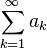 называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 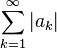 .
.
Ряд 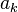 сходится абсолютно тогда и только тогда, когда сходятся оба положительных ряда
сходится абсолютно тогда и только тогда, когда сходятся оба положительных ряда 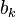 и
и 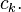 Где
Где 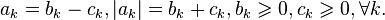
Доказательство. Если сходится 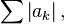 то по признаку сравнения тем более сходятся
то по признаку сравнения тем более сходятся 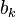 и
и 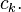 Наоборот, если сходятся
Наоборот, если сходятся 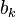 и
и 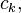 то сходится и их сумма
то сходится и их сумма 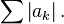
2) Свойства сходящихся рядов. Достаточный признак сходимости знакоположительных рядов.
Теорема 1 (необходимые условия сходимости ряда). Если ряд сходится, то последовательность его членов стремится к нулю.
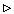 Если ряд
Если ряд  un сходится, т. е. существует конечный предел
un сходится, т. е. существует конечный предел 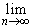 sn его частичных сумм, то из равенства
sn его частичных сумм, то из равенства
|
|
|
un = sn - sn -1, n = 2, 3,...,
следует, что
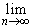 un =
un = 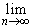 sn -
sn - 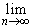 sn -1 = s - s = 0.
sn -1 = s - s = 0.
Пример. Ряд (30.5), членами которого являются члены геометрической прогрессии { qn }, в случае, когда знаменатель прогрессии q по абсолютной величине не менее единицы, т. е. | q | > 1, q 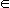 C, расходится, так как последовательность его членов { qn }не стремится к нулю, ибо | qn | > 1.
C, расходится, так как последовательность его членов { qn }не стремится к нулю, ибо | qn | > 1.
Теорема 2. Если ряды 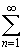 un и
un и 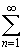 vn сходятся, то для любых
vn сходятся, то для любых 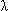
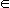 C,
C, 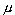
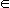 C ряд
C ряд 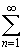 (
(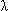 un +
un + 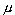 vn) сходится и
vn) сходится и
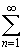 (
(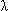 un +
un + 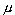 vn) =
vn) = 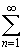
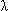 un +
un + 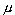
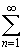 vn.
vn.
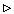 Положим sn =
Положим sn = 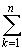 uk,
uk, 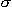 n =
n = 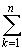 vk, тогда
vk, тогда
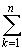 (
(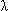 uk +
uk + 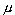 vk) =
vk) = 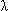 sn +
sn + 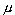
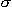 n
n
Если ряды 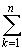 uk и
uk и 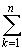 vk сходятся, т. е. существуют конечные пределы
vk сходятся, т. е. существуют конечные пределы 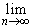 sn =
sn = 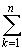 uk и
uk и 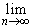
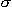 n =
n = 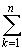 vk, то существует и конечный предел
vk, то существует и конечный предел
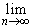
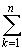 (
(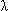 uk +
uk + 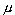 vk) =
vk) = 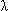
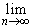 sn +
sn + 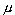
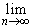
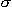 n =
n = 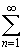
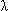 un +
un + 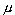
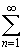 vn.
vn.
что и означает справедливость утверждения теоремы. 
Определение 2. Для ряда 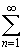 un ряд
un ряд
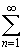 un+k
un+k
называется n-м остатком данного ряда.
Если n -и остаток ряда сходится, то его сумму будем обозначать rn, т. е.
rn = 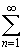 un+k. un+k.
| (30.6) |
Теорема 3. Если ряд сходится, то и любой его остаток сходится. Если какой-то остаток ряда сходится, то сам ряд также сходится, причем, если
s = 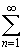 un. sn = un. sn = 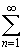 uk. rn = uk. rn = 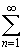 un+k, un+k,
| (30.7) |
то при любом n = 1, 2,...
| s = sn + rn. | (30.7) |
Пусть sn и 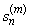 являются соответственно n -й частичной суммой ряда
являются соответственно n -й частичной суммой ряда 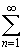 un и m -й частичной суммой его остатка (30.6):
un и m -й частичной суммой его остатка (30.6):
sn = u 1 + u 2 +... + un, 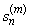 = un +1 + un +2 +... + un+m;
= un +1 + un +2 +... + un+m;
тогда
sn+m = sn + 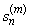 . .
| (30.8) |
Поэтому при произвольно фиксированном n пределы 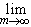 sn+m и
sn+m и 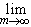
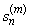 одновременно существуют или не существуют. Существование первого из этих пределов означает сходимость ряда
одновременно существуют или не существуют. Существование первого из этих пределов означает сходимость ряда 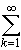 uk, а существование второго - сходимость остатка (30.6)
uk, а существование второго - сходимость остатка (30.6) 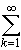 un+k этого ряда. Если оба рассматриваемых предела существуют, то, перейдя к пределу при m
un+k этого ряда. Если оба рассматриваемых предела существуют, то, перейдя к пределу при m 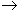
 в равенстве (30.8), получим формулу (30.7).
в равенстве (30.8), получим формулу (30.7).
Отметим, что если ряд 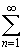 un сходится, то его остатки стремятся к нулю. Это сразу следует из формулы (30.7), так как сходимость ряда означает, что
un сходится, то его остатки стремятся к нулю. Это сразу следует из формулы (30.7), так как сходимость ряда означает, что 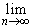 sn = s, и поэтому
sn = s, и поэтому
|
|
|
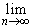 rn
rn 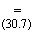
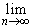 (s - sn) = 0.
(s - sn) = 0.
3) Признак Д’Аламбера. Радикальный признак Коши.
Признак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда
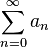
существует такое число 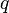 ,
, 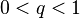 , что, начиная с некоторого номера, выполняется неравенство
, что, начиная с некоторого номера, выполняется неравенство
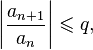
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
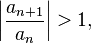
то ряд расходится.
Радикальный признак Коши — признак сходимости числового ряда:
Если для числового ряда
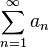 с неотрицательными членами существует такое число
с неотрицательными членами существует такое число 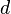 , , 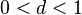 , что, начиная с некоторого номера, выполняется неравенство , что, начиная с некоторого номера, выполняется неравенство 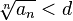 , то данный ряд сходится. , то данный ряд сходится.
|
4) Интегральный признак Коши-Маклорена.
Интегральный признак Коши́ – Макло́рена — признак сходимости убывающего положительного числового ряда. Признак Коши – Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на 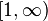 , последний часто может быть найден в явном виде.
, последний часто может быть найден в явном виде.
Пусть для функции f(x) выполняется:
-
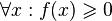 (функция принимает неотрицательные значения)
(функция принимает неотрицательные значения) -
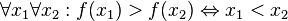 (функция монотонно убывает)
(функция монотонно убывает) -
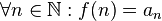 (соответствие функции ряду)
(соответствие функции ряду)
Тогда ряд 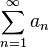 и несобственный интеграл
и несобственный интеграл 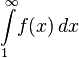 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
- Построим на графике f(x) ступенчатые фигуры как показано на рисунке
- Площадь большей фигуры равна
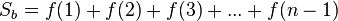
- Площадь меньшей фигуры равна
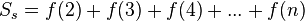
- Площадь криволинейной трапеции под графиком функции равна
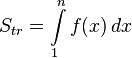
- Получаем
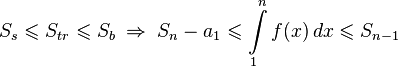
- Далее доказывается с помощью критерия сходимости знако-положительных рядов.
5) Знакопеременные ряды. Их свойства.
Ряды, не являющиеся знакопостоянными (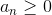 или
или 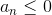 ) называются знакопеременными.
) называются знакопеременными.
Например, 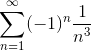 - знакочередующийся ряд,
- знакочередующийся ряд, 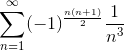 - знакопеременный ряд.
- знакопеременный ряд.
6) Знакочередующиеся ряды. Признак Лейбница.
Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
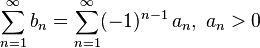
Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
Пусть для знакочередующегося ряда
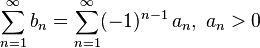 выполняются следующие условия:
выполняются следующие условия:
|
Замечания:
Если, выполнены все условия, и ряд из модулей (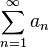 ) сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно. Строгая положительность
) сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно. Строгая положительность 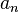 существенна.
существенна.
Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.
7) Признаки сравнения знакоположительных рядов.
8) Функциональные ряды. Степенные ряды.
Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция 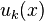 .
.
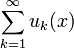
Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:
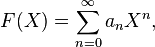
в котором коэффициенты 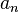 берутся из некоторого кольца
берутся из некоторого кольца 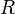 .
.
9) Теорема Абеля о сходимости степенного ряда.
Теорема Абеля — результат теории степенных рядов, названный в честь норвежского математика Нильса Абеля. Обратной к ней является теорема Абеля — Таубера.
Пусть 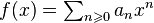 — степенной ряд с комплексными коэффициентами и радиусом сходимости
— степенной ряд с комплексными коэффициентами и радиусом сходимости 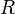 .
.
Если ряд 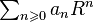 является сходящимся, тогда:
является сходящимся, тогда:
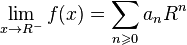 .
.
Доказательство
Заменой переменных 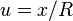 , можно считать
, можно считать 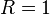 . Также (необходимым подбором
. Также (необходимым подбором 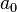 ) можно предположить
) можно предположить 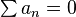 . Обозначим
. Обозначим 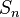 частичные суммы ряда
частичные суммы ряда 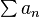 . Согласно предположению
. Согласно предположению 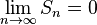 и нужно доказать, что
и нужно доказать, что 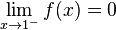 .
.
Рассмотрим 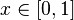 . Тогда (приняв
. Тогда (приняв  ):
):
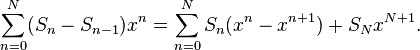
Отсюда получается 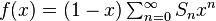 .
.
Для произвольного 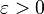 существует натуральное число
существует натуральное число 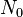 , что
, что 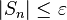 для всех
для всех 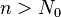 , поэтому:
, поэтому:
|
|
|
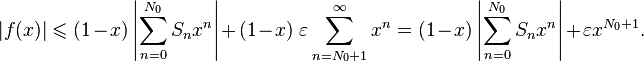
Правая часть стремится к  когда
когда 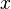 стремится к 1, в частности она меньше
стремится к 1, в частности она меньше 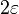 при следовании
при следовании 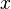 к 1.
к 1.
10) Ряды Тейлора и Маклорена.
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.
Ряд Тейлора был известен задолго до публикаций Тейлора[1] — его использовали ещё в XVII веке Грегори, а также Ньютон.
Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Пусть функция 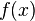 бесконечно дифференцируема в некоторой окрестности точки
бесконечно дифференцируема в некоторой окрестности точки 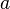 . Формальный ряд
. Формальный ряд
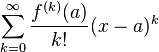
называется рядом Тейлора функции 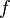 в точке
в точке 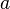 .
.
То есть, рядом Тейлора для функции 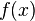 в окрестности точки
в окрестности точки 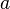 называется степенной ряд относительно двучлена
называется степенной ряд относительно двучлена 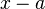 вида
вида 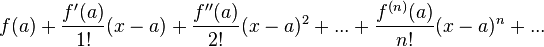 [2]
[2]
- В случае, если
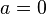 , этот ряд также называется рядом Маклорена.
, этот ряд также называется рядом Маклорена.
11) Радиус сходимости. Интервал, область сходимости степенного ряда. 12) Приближенное вычисление интегралов через ряды. 13) Тригонометрический ряд Фурье.
Тригонометрический ряд Фурье — представление произвольной функции 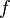 с периодом с периодом 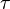 в виде ряда в виде ряда
или используя комплексную запись, в виде ряда:
Тригонометрическим рядом Фурье функции
где
Числа Ряд (1) сходится к функции
то их среднеквадратичное отклонение от функции
Несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. |
 2015-06-05
2015-06-05 862
862
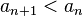 (монотонное убывание {an})
(монотонное убывание {an})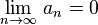 .
.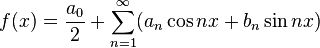
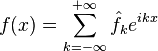 .
.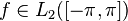 называют функциональный ряд вида
называют функциональный ряд вида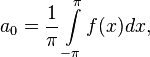
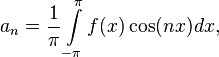
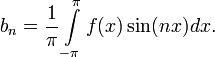
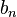 (
(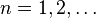 ) называются коэффициентами Фурье функции
) называются коэффициентами Фурье функции 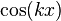 и проинтегрировать по промежутку
и проинтегрировать по промежутку 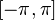 , благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент
, благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент 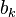
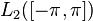 . Иными словами, если обозначить через
. Иными словами, если обозначить через 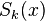 частичные суммы ряда (1):
частичные суммы ряда (1):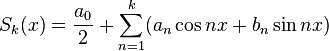 ,
,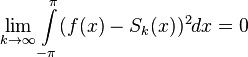 .
.