Пусть 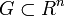 — открытое множество и на
— открытое множество и на 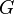 заданы функции
заданы функции 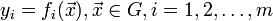 . Пусть
. Пусть 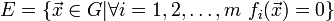 .
.
Эти 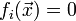 уравнения называют уравнениями связей (терминология позаимствована из механики).
уравнения называют уравнениями связей (терминология позаимствована из механики).
Пусть на 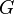 определена функция
определена функция 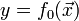 . Точка
. Точка 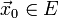 называется точкой условного экстремума функции
называется точкой условного экстремума функции 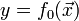 относительно уравнений связи, если она является точкой обычного экстремума
относительно уравнений связи, если она является точкой обычного экстремума 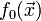 на множестве E (рассматриваются окрестности
на множестве E (рассматриваются окрестности 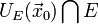 ).
).
Теорема: Пусть 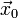 — точка условного экстремума функции
— точка условного экстремума функции 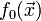 при выполнении уравнений связи. Тогда в этой точке
при выполнении уравнений связи. Тогда в этой точке 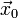 градиенты
градиенты 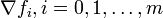 являются линейно зависимыми, то есть
являются линейно зависимыми, то есть 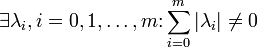 но
но 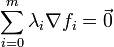 .
.
Следствие: Если 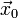 — точка условного экстремума функции
— точка условного экстремума функции 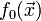 относительно уравнений связи, то
относительно уравнений связи, то 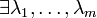 такие, что в точке
такие, что в точке 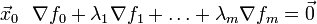 или в координатном виде
или в координатном виде 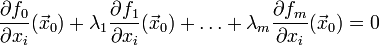 .
.
Достаточное условие условного экстремума: Пусть 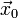 является стационарной точкой функции Лагранжа
является стационарной точкой функции Лагранжа 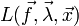 при
при 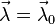 . Если
. Если 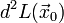 — отрицательно (положительно) определена квадратическая форма переменных
— отрицательно (положительно) определена квадратическая форма переменных 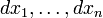 при условии
при условии 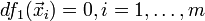 , то
, то 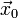 является точкой max (min для положительно определенной) условного экстремума. Если она при этих условиях не является знакоопределенной, тогда экстремума нет.
является точкой max (min для положительно определенной) условного экстремума. Если она при этих условиях не является знакоопределенной, тогда экстремума нет.
|
|
|
18) Производная функции по направлению.
В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.
Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.
Рассмотрим функцию 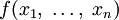 от
от 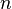 аргументов в окрестности точки
аргументов в окрестности точки 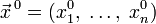 . Для любого единичного вектора
. Для любого единичного вектора 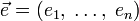 определим производную функции
определим производную функции 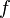 в точке
в точке 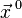 по направлению
по направлению 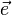 следующим образом:
следующим образом:
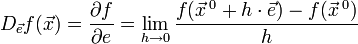
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора 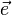 .
.
Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.
 2015-06-05
2015-06-05 482
482








