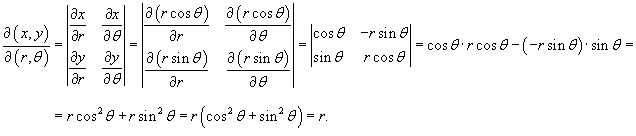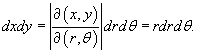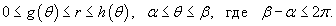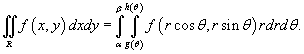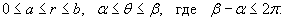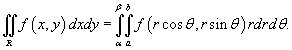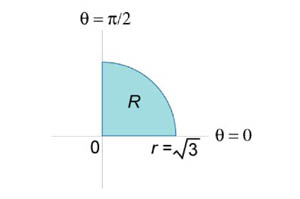Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
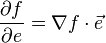
Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке.
19) Градиенты функции двух переменных.
20) Двойной интеграл. Геометрический и физический смысл.
Двойным интегралом называют кратный интеграл с 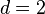 .
.
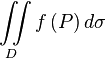 . Здесь
. Здесь 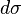 — элемент площади в рассматриваемых координатах.
— элемент площади в рассматриваемых координатах.
В прямоугольных координатах: 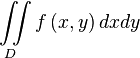 , где
, где 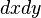 — элемент площади в прямоугольных координатах.
— элемент площади в прямоугольных координатах.
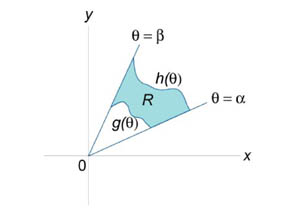
Геометрический смысл двойного интеграла:
Пусть функция 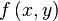 принимает в области
принимает в области  только положительные значения. Тогда двойной интеграл
только положительные значения. Тогда двойной интеграл 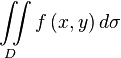 численно равен объему
численно равен объему 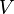 вертикального цилиндрического тела, построенного на основании
вертикального цилиндрического тела, построенного на основании 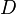 и ограниченного сверху соответствующим куском поверхности
и ограниченного сверху соответствующим куском поверхности 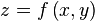
21) Вычисление двойного интеграла по прямоугольной области.
Пусть область интегрирования R представляет собой прямоугольник 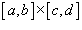 . Тогда двойной интеграл в такой области выражается через повторный интеграл в следующем виде:
. Тогда двойной интеграл в такой области выражается через повторный интеграл в следующем виде:
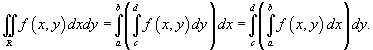
В данном случае область интегрирования R относится одновременно к типу I и II, так что у нас есть возможность выбирать, по какой переменной (x или y) начинать интегрировать функцию f (x,y). Обычно удобнее начинать с более простого интеграла.
В частном случае, когда подынтегральная функция f (x,y) "расщепляется" на произведение f (x) g (y), двойной интеграл равен произведению двух определенных интегралов:
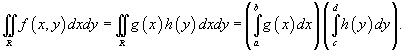
Вычислить двойной интеграл 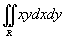 в области
в области 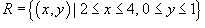 .
.
Решение.
Как видно, подынтегральная функция f (x,y) представляет собой произведение f (x) g (y). Следовательно, интеграл равен
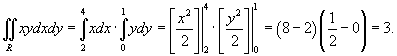
22) Вычисление двойного интеграла в полярных координатах.
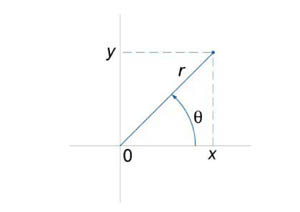
Одним из частных случаев замены переменных является переход из декартовой в полярную систему координат (рисунок 1). 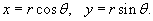
Якобиан такого преобразования имеет вид
Следовательно, дифференциальный элемент в полярных координатах будет равен
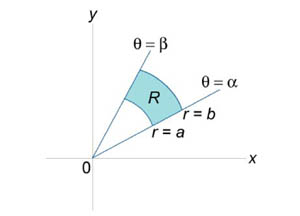
Пусть область интегрирования R в полярных координатах определяется следующим образом (рисунок 2):
Тогда двойной интеграл в полярных координатах описывается формулой
Будем называть полярным прямоугольником область интегрирования, показанную на рисунке 3 и удовлетворяющую условиям
В этом случае формула замены переменных в двойном интеграле имеет вид
Будьте внимательны, чтобы не пропустить сомножитель (якобиан) r в правой части этой формулы!
| ||||||||||||
| Пример 1: | ||||||||||||
Вычислить двойной интеграл 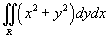 , преобразовав его в полярные координаты. Область интегрирования R представляет собой сектор , преобразовав его в полярные координаты. Область интегрирования R представляет собой сектор 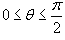 круга радиусом круга радиусом 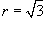 . Решение. Область R в полярных координатах описывается множеством . Решение. Область R в полярных координатах описывается множеством 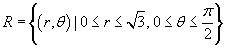 (рисунок 4). Применяя формулу (рисунок 4). Применяя формулу 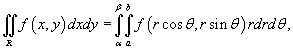 получаем получаем 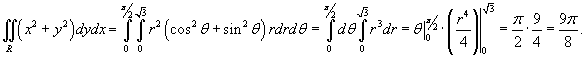 |
 2015-06-05
2015-06-05 739
739