Тройным интегралом называют кратный интеграл с 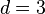 :
:
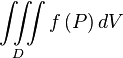
где 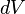 — элемент объема в рассматриваемых координатах
— элемент объема в рассматриваемых координатах
24) Криволинейный интеграл 1 рода.
Пусть кривая C описывается векторной функцией 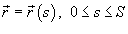 , где переменная s представляет собой длину дуги кривой (рисунок 1).
, где переменная s представляет собой длину дуги кривой (рисунок 1).
Если на кривой C определена скалярная функция F, то интеграл 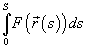 называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как
называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как
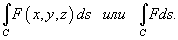
Криволинейный интеграл 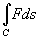 существует, если функция F непрерывна на кривой C.
существует, если функция F непрерывна на кривой C.
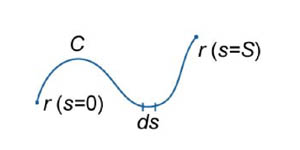 |  | |
| Рис.1 | Рис.2 |
Свойства криволинейного интеграла первого рода
Криволинейный интеграл I рода обладает следующими свойствами:
- Интеграл не зависит от ориентации кривой;
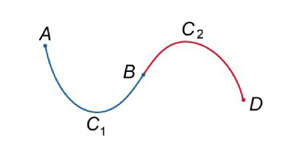
- Пусть кривая C 1 начинается в точке A и заканчивается в точке B, а кривая C 2 начинается в точке B и заканчивается в точке D (рисунок 2). Тогда их объединением будет называться кривая C 1 U C 2, которая проходит от A к B вдоль кривой C 1 и затем от B к D вдоль кривой C 2. Для криволинейных интегралов первого рода справедливо соотношение
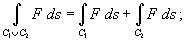
- Если гладкая кривая C задана параметрически соотношением
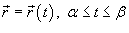 и скалярная функция F непрерывна на кривой C, то
и скалярная функция F непрерывна на кривой C, то
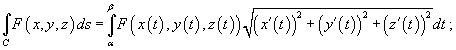
- Если C является гладкой кривой в плоскости O xy, заданной уравнением
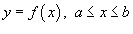 , то
, то
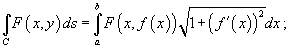
- Если гладкая кривая C в плоскости O xy определена уравнением
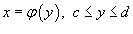 , то
, то
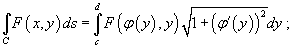
- В полярных координатах интеграл
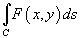 выражается формулой
выражается формулой
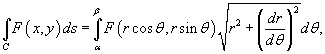
где кривая C задана в полярных координатах функцией 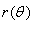 .
.
25) Криволинейный интеграл 2 рода.
Предположим, что кривая C задана векторной функцией 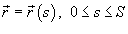 , где переменная s − длина дуги кривой. Тогда производная векторной функции
, где переменная s − длина дуги кривой. Тогда производная векторной функции
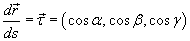
представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок 1).
В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осейO x, O y и O z, соответственно.
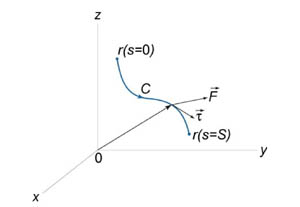 | 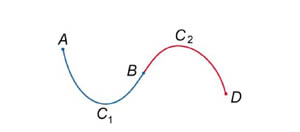 | |
| Рис.1 | Рис.2 |
Введем векторную функцию 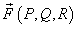 , определенную на кривой C, так, чтобы для скалярной функции
, определенную на кривой C, так, чтобы для скалярной функции
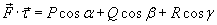
существовал криволинейный интеграл 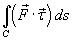 . Такой интеграл
. Такой интеграл 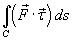 называется криволинейным интегралом второго рода от векторной функции
называется криволинейным интегралом второго рода от векторной функции 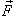 вдоль кривой C и обозначается как
вдоль кривой C и обозначается как
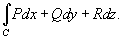
Таким образом, по определению,
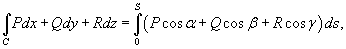
Где 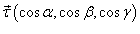 − единичный вектор касательной к кривой C.
− единичный вектор касательной к кривой C.
Последнюю формулу можно переписать также в векторной форме:

Где 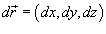 .
.
Если кривая C лежит в плоскости O xy, то полагая R = 0, получаем
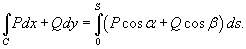
Свойства криволинейного интеграла второго рода
Криволинейный интеграл II рода обладает следующими свойствами:
- Пусть C обозначает кривую с началом в точке A и конечной точкой B. Обозначим через −C кривую противоположного направления - от B к A. Тогда
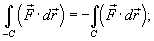
- Если C − объединение кривых C 1 и C 2 (рисунок 2 выше), то
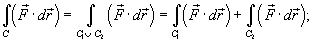
- Если кривая C задана параметрически в виде
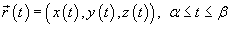 , то
, то
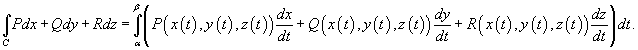
- Если кривая C лежит в плоскости O xy и задана уравнением
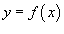 (предполагается, что R = 0и t = x), то последняя формула записывается в виде
(предполагается, что R = 0и t = x), то последняя формула записывается в виде
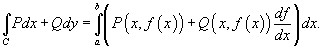
26) Формула Остроградского-Грина и ее приближение к вычислению интеграла по замкнутому контуру.
27) Дивергенция векторного поля.
Дивергенция (от лат. divergere — обнаруживать расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки. Если учесть, что потоку можно приписать алгебраический знак, то нет необходимости учитывать входящий и исходящий потоки по отдельности, всё будет автоматически учтено при суммировании с учётом знака. Поэтому можно дать более короткое определение дивергенции: дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой (в условиях конкретной задачи) окрестности каждой внутренней точки области определения поля.
Оператор дивергенции, применённый к полю 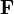 , обозначают как
, обозначают как 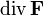 или
или
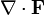 .
.
Определение дивергенции выглядит так:

где Ф F — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объём V. Ещё более общим, а потому удобным в применении, является определение, когда форма области с поверхностью S и объёмом V допускается любой. Единственным требованием является её нахождение внутри сферы радиусом, стремящимся к нулю (то есть чтобы вся поверхность находилась в бесконечно малой окрестности данной точки, что нужно, чтобы дивергенция была локальной операцией и для чего очевидно недостаточно стремления к нулю площади поверхности и объёма ее внутренности). В обоих случаях подразумевается, что
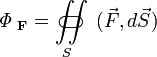 .
.
Пусть задано векторное поле 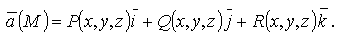
Дивергенцией или расходимостью векторного поля  называется скалярная функция, определяемая равенством:
называется скалярная функция, определяемая равенством:
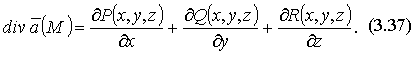
На этот раз векторное поле  порождает скалярное поле div
порождает скалярное поле div  .
.
С учетом понятий дивергенции и потока векторного поля формулу Остроградского можно представить в форме:
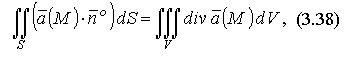
т. е. поток векторного поля  через замкнутую поверхность S в направлении внешней нормали равен тройному интегралу от дивергенции векторного поля по области, ограниченной этой поверхностью.
через замкнутую поверхность S в направлении внешней нормали равен тройному интегралу от дивергенции векторного поля по области, ограниченной этой поверхностью.
На основании формулы (3.38) можно записать: 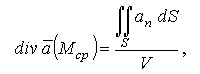 и, переходя к пределу, стягивая V в точку М (при этом величина V → 0), имеем:
и, переходя к пределу, стягивая V в точку М (при этом величина V → 0), имеем:
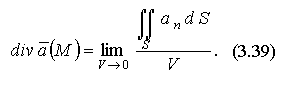
То есть div  есть предел отношения потока поля
есть предел отношения потока поля  через бесконечно малую замкнутую поверхность, окружающую точку М, к величине объёма, ограниченного этой поверхностью. Из этого следует, что дивергенция не зависит от выбора системы координат.
через бесконечно малую замкнутую поверхность, окружающую точку М, к величине объёма, ограниченного этой поверхностью. Из этого следует, что дивергенция не зависит от выбора системы координат.
Если поток 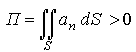 , то в область V втекает большее количество жидкости (если следовать ранее рассмотренному примеру о течении несжимаемой жидкости), чем вытекает из неё, т.е. внутри области V имеются источники жидкости.
, то в область V втекает большее количество жидкости (если следовать ранее рассмотренному примеру о течении несжимаемой жидкости), чем вытекает из неё, т.е. внутри области V имеются источники жидкости.
Если П < 0, то внутри области V есть стоки.
Но поток векторного поля характеризует интенсивность источников и стоков лишь суммарно, т.е. при П ≥ 0 внутри области V могут быть как источники, так и стоки.
Для характеристики точки можно использовать div  .
.
Если div  > 0, то данная точка есть источник, если div
> 0, то данная точка есть источник, если div  < 0 – то сток.
< 0 – то сток.
Заметим, что div  можно записать с помощью символического вектора Гамильтона
можно записать с помощью символического вектора Гамильтона
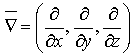 в следующем виде:
в следующем виде:
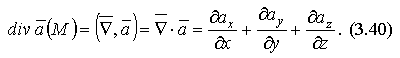
Отметим свойства дивергенции (справедливость которых рекомендуется показать самостоятельно):
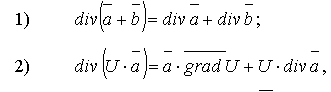
где U – скалярная функция.
 2015-06-05
2015-06-05 1037
1037
