2017-12-14
653
Случайная величина Х (одномерная) – величина, которая может принять различные вероятные значения х на некотором интервале (-¥£ х £¥), т.е. х – возможное значение с.в. Х.
Случайная величина может быть дискретной и непрерывной. Вероятностные свойства с.в. Х характеризуются интегральной функцией распределения Р(x). Значение функции Р(x) равно вероятности обнаружить с.в. Х<х (или, что то же, на интервале ‑¥, х), т.е. Р(x)=Prob(X<x), где х – конкретная детерминированная величина.
Если с.в. Х может принимать лишь дискретные значения х 1, х 2,... х n с вероятностями р 1, р 2,... р n, то функция распределения представляет собой сумму вероятностей тех значений х k, которые меньше х.
. (3.1)
На рисунке Prob(X£x 3 )=Р (х 3)=0,5 (т.е. Х = х 1 или Х=х 2 или Х=х 3). Prob (X=x 4)=0,6–0,5=0,1 (скачок равен вероятности появления значения х 4).
Функция распределения числа m наступления события в последова-тельности n независимых испытаний, согласно формуле (2.17).
Биномиальный закон распре-деления:
(3.2)
. (Математическое (м.о.) ожидание и дисперсия с.в.)
|
|
|
Если с.в. Х непрерывна, то функция распределения имеет колоколообразный вид, показанный на рисунке.
Наиболее часто для описания распределения случайных величин используется нормальное или гауссово распределение:
.
|
Коэффициент нормирует площадь кривой распределения симметричной относительно 
(центра распределения или м.о.), 
, а 
– дисперсия, характеризирующая разброс с.в. относительно м.о. в виде средне квадратичного отклонения (стандарта с.в.) 
.
Интегральная кривая нормального распределения:
, где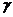 
– новая переменная 
,
а 
– интеграл вероятности Гаусса.
Свойства функции распределения:
1) Р(х) – неубывающая функция аргумента х
(т.е. при x2>x1 P(x2)=Prob(X<x2)>P(x1)=Prob(X<x1));
2) при x=-¥ P(x) =0;
3) при x=+¥ P(x)= 1;
4) Prob(x1<X£x2)=P(x2)–P(x1); (3.3)
5) Prob(X=x1)= 0.
Вероятность обнаружить число, например, 241.000...¥, равно 0. Однако, делая измерения, мы округляем значения, тем самым, увеличивая вероятность их появления. Например, округленное 241.0 содержит значения от 240.9500...¥ до 241.04999... ¥ и вероятность попадания числа в этот интервал не равна 0.
Распределение с.в. Х характеризуется также функцией плотности распределения с.в. (р(х)). Для дискретных значений с.в. функция плотности распределения может задаваться таблично. График функции р(х)=рi при x=xi изображен на рисунке.
Так как возможные значения с.в. x i образуют полную группу несов-местных событий (т.е. в каждом из n испытаниях с.в. обязательно примет одно из значений x i с определенной вероятностью), то 
, где n – число
испытаний.
Для непрерывной с.в. функция плотности распределения имеет вид, показанный на рисунке.
|
|
|
Если функция распределения с.в. Р(х) – непрерывна, то
, (3.4)
или 
. По непрерывной кривой плотности распределения, в отличие от дискретной, вероятность обнаружить точное число х 2 равна нулю. При помощи функции р(х) вероятность обнаружить с.в. Х в бесконечно малом интервале x<X<x+dx равна Pro b(x<X<x+dx)=p(x)dx (площадь прямоугольника, dx ®0). То же в конечном интервале x1<X<x2:
. (3.5)
Геометрически это заштрихованная площадь под кривой плотности распределения.
Из (3.4) следует, что
, (3.6)
поэтому функцию распределения называют еще интегральной функцией распределения.
