Для получения второго уравнения используем свойство корней исходного уравнения

Из исходного уравнения b = - (X₁ + X₂ + X₃) → b = - (g₁ + g₂ - ih + g₂ + ih)

→ b = - (g₁ + 2g₂)

6. X₁ = g₁ =  - b)

→                 X₁₁ = g₁₁ =  - b)

→                 X₁₂ = g₁₂ =  - b)

7. → g₂ = -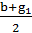

→ g₂₁ = -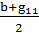

→ g₂₂ = -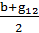

8. Определяем два остальных корня

X₂₁ = g₂₁ + h

X₂₂ = g₂₂ + h

X₃₁ = g₂₁ – h

X₃₂ = g₂₂ – h

Пример 9 Решить уравнение с помощью формул системы mn параметров

x3 - 6x2 + 58x – 200 = 0

где a =1, b = - 6, c = 58, d = - 200

 

Решение

1. Определяем значение D₁ = -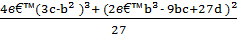

-→D₁ = - [4(174 – 36)3+(- 432 + 3132 – 5400)2]/27 = - [ 10512288 + 7290000 ]/27= 659344

-→ D₁ = [(g₁ - g₂)² - h² ]² ∙ 4h² = 659344 = 4∙2²∙7²∙29² = 4∙14²∙29² = 4∙7²∙58² = 4∙2²∙203²

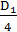-→  = 203²∙2² = 58²∙7² = 29²∙14²

Пусть h₁² = 7²

→ X₁ = g₁₁ =  - b) =  + 6) =  = 4

→ X₁ = 4

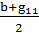→ g₂₁ = -  = -  = 1

→ X_2,3 = g₂₁ + ih₁ = 1 ± 7i → X₂ = 1 - 7i, X₃ = 1 + 7i

 

Задача решена!

Пример 10 Дано уравнение

x3 - 6x2 + 21x – 52 = 0

где a =1, b = - 6, c = 21, d = - 52

Решить уравнение с помощью формул системы mn параметров

 

Решение

1. Определяем значение D₁ = -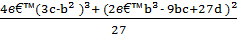

-→D₁ = - [4(63 – 36)3+(- 432 + 1134 – 1404)2]/27 = - [ 78732 + 492804 ]/27= 21168

→ D₁ = [(g₁ - g₂)² - h² ]² ∙ 4h² = 21168 = 4∙2²∙7² ∙  = 4∙14²∙  = 4∙

→ D₁ =

 

Пусть h₁² =

→ X₁ = g₁₁ =  - b) =  + 6) =  = 4

→ X₁ = 4

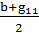→ g₂₁ = -  = -  = 1

→ X_2,3 = g₂₁ + ih₁ = 1 ± 2i  → X₂ = 1 + 2i  , X₃ = 1 - 2i

Сравните метод решения и результат с первоисточником.

[И.Н.Бронштейн. К. А.Семендяев.Справочник по математике. М. Наука.1980. Стр. 220 ]

 

Вывод новых формул

Основные свойства корней квадратного и кубического уравнений выражаются известными формулами Виета. Использование системы mn параметров дает возможность получения новых, ранее неизвестных, формул отражающих свойства корней указанных уравнений.

Рассмотрим кубическое уравнение и проведем анализ формулы (1)

(2mn)² + (3x + b)(2mn) + 3x² + 2bx +с = 0

Если в это уравнение подставить значение любого из корней исходного кубического уравнения, то получим

 

(2mn)² + (3x_i + b)(2mn) + 3x_i² + 2bx_i +с = 0

→ (2mn)² + (3x₁ + b)(2mn) + 3x₁² + 2bx₁ +с = 0

→ (2mn)² + (3x₂ + b)(2mn) + 3x₂² + 2bx₂ +с = 0

→ (2mn)² + (3x₃ + b)(2mn) + 3x₃² + 2bx₃ +с = 0

 

Таким образом, исходное кубическое уравнение распадается на три квадратных уравнения. При этом для каждого положительного значения (2mn)_I обязательно найдется отрицательное значение (2mn)_j. Поэтому общая сумма всех корней вида (2mn) будет равна нулю.

→ (3x₁ + b) + (3x₂ + b) + (3x₃ + b) = 0 → 3(x₁ + x₂ + x₃ ) = - 3 b

→ (x₁ + x₂ + x₃ ) = - b.

Таким образом получили строгое доказательство одного из уравнений Виета.

Рассмотрим любых два уравнения, например,

→ (2mn)² + (3x₁ + b)(2mn) + 3x₁² + 2bx₁ +с = 0

(2mn)² + (3x₂ + b)(2mn) + 3x₂² + 2bx₂ +с = 0.

Здесь в качестве свободных членов имеем 3x₁² + 2bx₁ +с и 3x₂² + 2bx₂ +с. Их сумма равна

→ Σ = 3(x₁² + 3x₂²) + 2 b(x₁ + x₂) + 2 с. Расчеты показывают, что

3(x₁² + x₂²) + 2 b(x₁ + x₂) + 2 с = (x₁ - x₂)²

→ (x₁ + x₂)² + b(x₁ + x₂) + с - x₁∙ x₂ = 0

Тогда для трех корней исходного уравнения будем иметь

→ (x₁ + x₂)² + b(x₁ + x₂) + с - x₁∙ x₂ = 0

→ (x₁ + x₃)² + b(x₁ + x₃) + с - x₁∙ x₃ = 0

→ (x₂ + x₃)² + b(x₂ + x₃) + с - x₂∙ x₃ = 0

Это новые формулы, отражающие свойства корней исходного кубического уравнения!