2020-10-09
169
Точка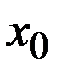 
называется точкой максимума функции 
, если 
, для любых значений 
из 
-окрестности (достаточно малой окрестности) точки 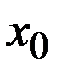. Значение функции в точке максимума называется максимумом функции (см. Рис 3.4).
Точка 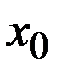называется точкой минимума функции , если 
, для любых значений из -окрестности (достаточно малой окрестности) точки 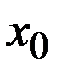. Значение функции в точке минимума называют минимумом функции (см. Рис 3.4).
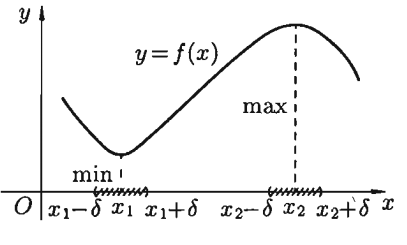
Рис 3.4
Точки максимума и минимума называют точками экстремума. Максимум и минимумфункции называют экстремумом.
Теорема 3.8. (Необходимые условия экстремума функции)
Если дифференцируемая функция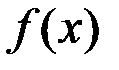 
имеет экстремум в точке 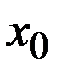, то ее производная в этой точке равна нулю: 
.
Геометрически условие означает, что в точке 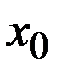существует касательная к графику функции, параллельная оси 
.
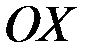Обратная теорема не верна: существуют точки, в которых производная равна нулю (касательная параллельна оси 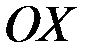), но эти точки не являются точками экстремума. Существуют функции, которые в точках экстремума не имеют производных. Непрерывная функция может иметь экстремум лишь в критических точках, где производная равна нулю или производная не существует. Эти точки еще называют подозрительными на экстремум.
Теорема 3.9. (Достаточные условия экстремума функции)
Если непрерывная функция 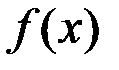дифференцируема в некоторой -окрестности критической точки 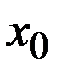и при переходе через нее (слева направо) производная меняет знак, то 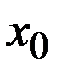– точка экстремума.
Если знак меняется с плюса на минус, то 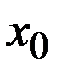– точка максимума (рис 8.5).
Если знак меняется с минуса на плюс, то 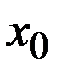– точка минимума (рис 8.6).
Исследовать функцию на экстремум означает найти все ее экстремумы.
Рис 3.5 Рис 3.6
