Пример 22. Пример 18. x-1 r0i (Vx-1) -------- = - ^ = li 1----- 1 lnx 0x^i (lnx)'

Пример 18.

x - 1 r0i (Vx - 1) -------- = - ^ = li 1----- 1 l nx 0 x^i (ln x)'

lim ---------- = - = lim

x

lim ₁ = lim — — = -

Пример	19.	1 - cos x r0^ (1С0s x) lim----------------- = - ^ = lim - ----- = x ^0 x 2 0 x ^0 (x 2) sin x 1 sin x г0^ = lim----------------- = - lim------------- = ^ - ^ = x ^0 2x 2 x ^0 x 0 1 (sin x)' 1 1 = - lim---------------------------- = - • 1 = -. 2 x ^0 x ' 2 2
Пример	20.	ex Г CXD ^ (ex)' ex lim — = — = lim ------- = lim — = +оо x ^+оо x СЮ x ^+оо x' x ^+оо 1
Пример	21.	ex Г CXD ^ (ex)' ex lim x 2 = — = lim = lim — = x ^+оо СЮ x ^+оо (x 2) x ^+оо 2 x
		гсю^ (ex) ex = — = lim ----- = lim — = +СЮ. сю x ^+оо 2 x ' x ^+оо 2
		a b ad
	3 b c

Г -1 ln x г сю ^ lim x ln x= <^ 0 • сю ^ = lim — = — ^0+0 x ^0+0 1 /x cю

ln x x ln x = 0 • сю = lim

x ^0+0

(ln x) 1 /x
= lim = lim - x ² = lim -x = 0 .

x ^0+0 (1/x) x ^0+0 - 1 / x ^0+0

в связи с последним примером отметим общее правило: пеопределеп-пость типа |0 • сю| всегда можно превратить в неопределенность тина \^ ₀ ^ или типа {^}, перенося один из сомножителей в знаменатель. После этого к ней можно применять правило Лопиталя.

Задача 21. Можно ли применять правило Лониталя для вычисления сле­дующих пределов:

ln(x — 1) x x?

lim--------------, lim —, lim --^

x—^2 x — 2 x ^+оо e^x x ^оо у x 2 +1

4.9 Производные высших порядков

Второй производной функции f называют производную от первой производной. Обозначение: f '' или y". Аналогично определяют третью, четвертую и т.д. производные. Обозначение для производной n -го поряд­ка: f^ⁿ^ или y^ⁿ\

Пример 23.

4.10 Производная обратной функции

Теорема 27. Пусть прямая функция f дифференцируема и f'(x) = 0. Тоща обратная функция f~^ дифференцируема и

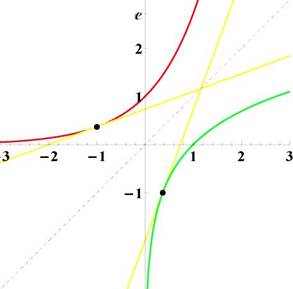
Доказательство. Напомним, что графики прямой и обратной функ­ций получаются друг из друга в результате отражения относительно пря­мой y = x, см. рис. 17, 21, 24, 27, 30, 33.

Надо заметить, что при отражении относительно прямой y = x ка­
сательная переходит в касательную. Но при этом тангенс угла наклона
меняется на котангенс. П

4.11 Дифференциал

Дифференциалом, функции y = F(x) называют произведение F'(x) на переменную dx:

dF = F'(x)dx.

или

dy = y'(x) dx.

Рис. 2: Отражение касательной относительно прямой y = x

Пример 24.

d(x^) = 2x • dx.

Для нас достаточно смотреть на дифференциал как на часть выраже­ния, появляющегося в обозначении интеграла. Но дифференциал имеет и свой собственный буквальный смысл. Дифференциал — это функция, зависящая от аргумента dx и параметра x и обозначаемая символом dF. Две буквы [dF и dx) в обозпачепии функции и ее аргумента не являются чем-то необычным; несколькими буквами обозначают многие элементар­ные функции, например. ln, sin. Здесь буква d в обозначении подчерки­вает, что dF и dx — ио смыслу очень маленькие (бесконечно малые) величины.

Из определения производной

F(x + ∆x) - F(x)

lim

∆x

F'(x)

имеем приближенное равенство

F'(x)

F(x + ∆x) - F(x)

причем чем меньше ∆ x, тем точнее это равенство. Или

F(x + ∆x) - F(x) ^ F'(x) ∆x.

Или

∆ F ^ F'(x) ∆x.

(4.4)

Если же в это равенство подставить "бесконечно малое" приращение аргумента dx^ то получим точное равенство

dF = F(x + dx) - F(x) = F'(x) dx,

являющееся определением дифференциала. Таким образом, дифферен­циал имеет смысл приращения функции, отвечающего "бесконечно ма­лому" ириращению аргумента.

Геометрический смысл дифференциала аналогичен геометрическому смыслу касательной: график дифференциала совпадает с касательной к ириращению функции ∆F(∆x) = F(x + ∆x) - F(x).