Теорема 18

lim

sin x

1.

Эту формулу называют первым замечательным, пределом,. Геомет­рический смысл состоит в том, что график синуса (рис. 15) пересекает начало координат иод 45⁰. Другой геометрический смысл: синус малень­кого угла почти совпадает с величиной угла, измеренной в радианах.

Следствие 19.

1 2

tg x

lim

1,

lim x 0

cos x

x→ 0 X

x ²

sin 3 x

Задача 8. Найти предел

lim

x

x 0

Решение. Имеем sin3ж lim---------- x→ 0 X

sin y

3 lim -------- = {у = 3ж } = 3 lim

x→ 0 3ж y→ 0 у

3.10 Второй замечательный предел

4 \x+2

x +4

Задача 9. Найти предел lim ₄ ^x _x ⁺ _- ⁴ ₁

а lim (ж+ 2) = + ∞. Здесь

Решение. Очевидно, что lim

x→ + ∞ 4ж - 1 4 x→ + ∞

x +2

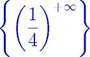
нет неопределенности. В силу свойств показательной функции имеем

lim

0.

x +4

x→ + ∞ 4 х - 1 Число е определяется по формуле

				x
e	= lim x →∞	1+	x	,

(3.1;

которую называют вторым зам,ечательным пределом., е ≈ 2,718. Его применяют для раскрытия неопределенностей типа { 1 ^∞}.

Следствие 20.

e = lim(1 + x)

x 0

log _a (1 + x) 1 ln(1 + x)

lim =, lim

x→Ь x ln a x→Q x

lim ------------ = ln a, lim -------------- = 1.

x→Q x x→Q x

Задача 10. Найти предел

3 x - 1
lim----------.

x→ О x

Решение. По первой формуле из следствия 20 имеем

3 x - 1
lim--------- = ln3.

x→Q x

Задача 11. Найти предел

4 x e^x

lim.

x→ О x

Решение. Вьшесем в числителе e^x за скобку и воспользуемся следстви­ем 20 второго замечательпого предела:

lim= lim=

x→Q x x→Q x

lim e x · e - 1 · 3 = e *^ · 1 · 3 = 3. П

x→ o 3 x

Теорема 21. Пусть предел lim(u (x)) представляет собой пеопреде-леппость вида { 1 ^∞ }. Тогда

lim(u (x)) v (x) = e i^"^— v (x)(u (x) - i) .

Глава 4

Производная

4.1 Определение производной

Производной функции y = f(x) в точке xq называют число, обозна­чаемое f'(xo) или y'(xо) и равное пределу

f (xо) = lim f(xo + ∆x) - f(xo) или для произвольной точки x

y (x + ∆x)-y(x) y (x) = lim

Ах^О ∆x

Производной функции f называют функцию, обозначаемую f ', кото­рая каждому x сопоставляет число f'(x).

4.2 Задачи, приводящие

к определению производной

Таких задач очень много. Но наиболее известны следующие две.

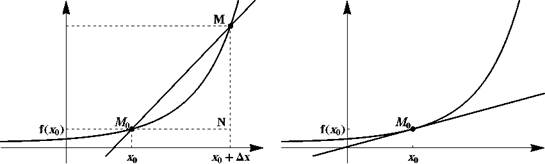
Пример 14. Рассмотрим график функции y = f(x). Зафиксируем на гра­фике точку M о(x о, f(xo)) и возьмем еще одну точку M(xо + ∆ x, f(xo + ∆x)). Проведем через них прямую. Прямую, проходящую через две точ­ки линии, называют секущей.

Пайдем угловой коэффициент секущей:

, NM f (x о + ∆ x) - f (x о)

*= = tg ϕ = MN = ∆ x.

Г(^о+Дх)

Рис. 1: Слева: секущая. Справа: касателвная

Предельное положение секущей, когда точка M стремится к точке M q, называют касательной. Когда M стремится к M q, угловой коэффициент превращается в число

f(xo + ∆x) - f(xo)

k

lim

(4.2;

∆x

Пример 15. Предел v(to) = lim — — А - ''^^ °^ называют мгновенной ско-ростью в момент времени to.

Таким образом, производная функции в точке xq совпадает с угловым коэффициентом касательной, а производная пути по времени совпадает с мгновенной скоростью.

4.3 Геометрический смысл производной; уравнение касательной

Согласно формулам (4.2) и (4.1) имеем

f'(xo) = kо

или словами: производная равна угловому коэффициенту касательной в точке касания. Это свойство называют геометрическим, сммслом про­изводной.

Задача 12. Составьте уравнение касательной к графику функции f, про­ходящей через заданную точку xq.

Решение. Уравнение касательной выпишем с помощью формулы

y -yо = kо(x -xо), 40

которая определяет прямую проходящую через точку (x ₀ ,y ₀) с угловым коэффициентом k ₀. Итак, уравнение касательной имеет вид

y- f(x0) = f'(x0)(x-x ₀ ).

(4.3)

П

4.4 Дифференцируемость

Функцию называют дифференцируемой в точке x, если она имеет про­изводную в этой точке. Геометрически дифференцируемость в точке x ₀ означает, что график функции имеет касательную в этой точке. См. пра­вый рис. 1 и рис. 9.

Функцию называют дифференцируемой., если она имеет производную во всех точках своей области определения.

4.5 Таблица производных

Теорема 22.
C =	0,
x =	1,
f 1 '
x	-x 2
(ax)' =	ax ln a,	a > 0,
(log a x)' =		a > 0 ,a = 1
, x ln a
(sin x)' =	cos x,
(tg x)' =
, cos2 x
(arcsin x)' =
√ 1 -x 2
(arctg x)' =
,

α 1

(x

(x

x

(ln x (cos x (ctg x

(arccos x (ar cct gx Пример 16. Найдем производные функций y = x ³ ^ y

αx 1

2 √x

x

x

sin x,

₂, sin x

л/1 - x ²

- 1+ x 2. x 3 / 2^ y = 2 x И

y = lgx.

3 x 2

(xα)' = αxα-1 =3x3-1

1 / 2 x, 2

3 / 2 - 1

x 3 / 2у

(xα) ' = αxα- 1

x

(x

(2 x)' = (a^x) = a^x l na=2^x l n2,

(lg x)= (log₁₀ x)' = (log ax)'

xlna x ln 10

Задача 13. Найдите производные функций y = e5, y = \ 7 и y = ln3.

Решение. Производные равны нулю. П

Правило: При вычислении производных выражения вида _x ¹, √ x^m и -1 ¹ ^, следует записывать как степени.

αx

имеем:

Задача 14. Найдите производные функций y = √ x и y Решение. Используя это правило и формулу (xα

√ x)

1\'

x

(x

(x

1 / 3у

2 / 3

x

x

1 / 3 - 1

(- 7) x^{- 7 - 1} = - 7 x^{- 8}.

4.6 Основные правила дифференцирования

Теорема 23. Пусть f и g дифференцируемы. Тогда

{f(x)±g(x))

(Cg(x))

f(x

C

{f(x)g(x))

{f(x)g(x)h(x))

f (x g(x)

f(x)±g (x), Cg'(x),

f (x) C, f'(x)g(x) + f(x)g'(x),

f(x)g(x)h(x) + f(x)g'(x)h(x) + f(x)g(x)h'(x) f ' (x)g(x) - f(x)g ' (x) g2(x)

Правило матрешек: при вычислепии производных в первую оче­редь дифференцируют действие, которое при вычислении функции вы­полняется последним.

Задача 15. Найдите производную функции y = x^e^x.

Решение. При вычислении этой функции последним действием выпол­няется умножение x^ на e^x. Поэтому прежде всего надо применить пра­вило дифференцирования произведения, а затем таблицу производных:

y' = (x'e^x) = {f(x)g(x)У = f (x)g(x) + f(x)g'(x) =

Задача 16. Найдите производную функции y = e_xл/xlnx.

Решение. Последнее действие — двойное умножение. Поэтому имеем

y' = (e_xл/x ln x)' = (f(x)g(x)h(x)) =

= f(x)g(x)h(x) + f(x)g'(x)h(x) + f (x)g(x)h'(x) =

= (e^x) л/x l nx + e^x (л/ x)'ln x + e^x л/ x (ln x)' =

_x√ _x 1 _x x

e x ln x + e 2 √x ln x + e x.

x - 1
Задача 17. Найдите производную функции y = ^ ----- в точке x = 1.

x ^ + 2

Решение. При вычислении этой функции последним действием выпол­няется деление x"^ - 1 на x ^ + 2. Поэтому прежде всего надо применить

f x)у f '{ x)g { x) - f { x)g '{ x)

g (x) g 2(x)

правило дифференцирования частного

x^- 1 > ff(x)y f(x)g(x)-f(x)g'(x)

y

x 2 + 2 g(x) g ² (x)

(x^ - 1) (x2 + 2) - (x^ - 1)(x2 + 2) =

(x 2 + 2)2

3 x 2(x 2 + 2) - (x^ - 1)2 x = x ^ + 6 x 2 + 2x

(x 2 + 2)2 (x 2 + 2)2 ,

1^ + 6 •12 + 2-1 9

y '(1

(12 + 2)2 32

Ответ: y'(1) = 1. П

Задача 18. Составьте уравнение касательной к графику функции y = x 2 - 12л x в точке xq = 4.

Решение. Сначала вычисляем производную:

1 6

y'(x) = (x 2 - 12лx) = 2x- 12^^ = 2x

2 x x

Затем вычисляем значения функции и производной в точке xq = 4:

y(xо) = x ₂ - 12л x ^ = 4 2 - 12\/4 = 16 - 24 = - 8,

y (xо) = 2 x о - ^ = 2-4 - — = 8 - 3 = 5 .
л/ x ^ V4

Мы оказались в условиях задачи 12. Подставляем в формулу

y- f(xo) = f(xo)(x-xo) паши данные xq = 4, y(xо) = - 8, y'(xо) = 5:

y- (- 8) = 5(x- 4).

Ответ: y = 5 x - 28.

4.7 Таблица производных с внутренней функцией

Теорема 24 (о производной сложной функции). Пусть f и u — диффе­ренцируемые функции. Тогда

f(u(x))) = f(u(x))u'(x). 44

Теорема 25 (таблица производных с виутреиией функцией). Пусть u дифференцируемая функция. Тогда

1 \' u'(x)

(u^(x)) = 2u (x)u'(x),

u (x)

u ²(x)

2^u(x)

(a

u (x) u (x)

(logau(x

(l nu (x

[cosu(x

{tgu(x

[ctgu(x

[ ar cs in u(x

(arccos u (x

(arctg u (x (arcctg u (x

u'(x)

u(x) ln a u'(x

a > 0 ,a = 1,

u (x)

sinu(x)

s in u (x) • u (x)

u'(x)

cos² u (x)

u'(x)

sin² u (x)

u'(x)

\J 1 — u^(x) u'(x) \J 1 — u^(x) u'(x) 1 + u?(x), u'(x) 1 + u?(x)

cosu(x) u'(x

Правило: Вычисление любой ироизводной начинают с ирименения правила матрешек: последнее выполняемое действие показывает, какой формулой надо пользоваться. Если последнее выполняемое действие ока­залось:

Ф функцией от x, то применяют обычную таблицу производных;

Ф функцией от другой функции., то применяют таблицу производных с внутренней функцией;

Ф ариф.мешической операцией^ применяют теорему 23.

Задача 19. Найдите производную функции y = e ^{3 x} +2.

Решение. При вычислении этой функции последней выполняется опе­рация взятия экспопепты от 3 x + 2. Эту операцию надо дифференци­ровать первой. Вводя обозначение u (x) = 3 x + 2, видим, что функцию y = e 3 x +2 jyjQjj^jjQ представить в виде y = e^ ^{( x )}:

y' = (e ^{3 x} +2)' = {u (x) = 3 x + 2 } = (e "(x))' =

Задача 20. Найдите производную функции y = \x2 + 6.

Решение. Нри вычислении этой функции последней выполняется опе­рация вычисления корня от x ² + 6. Вводя обозначение u (x) = x ² + 6,

u (x)

видим, что функцию y = л/x ² + 6 можно представить в виде y = \/'

y = (x 2 + 6)' = {u (x) = x 2 + 6 } = (\Ju(x))

u'(x) (x2 + 6)' 2x

2л/u (x) 2л/x2 + 6 2л/ x 2 + 6.

4.8 Правило Лопиталя

Теорема 26. Пусть предел lim Д^{( x )} представляет собой неопределеп-

пость ⁰ ₀ или ^. Тогда

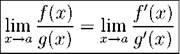
при условпп, что второй предел существует.

f (x) = g (x)

f(x) ff(x)y f(x)g(x)-f(x)g'(x)

g'(x) g(x) g2(x)

Пример 17.

0 0

lim	ax -
x^ 0	x
(ax -	1)'

lim ------------ = lim----------- = ln a.

x—^ 0 x ' x ^0 1