в кольце Р[х].
Определение 1. Многочлен f(x) ¹ 0 из Р[х] называется приводимым над полем Р, если его можно представить в виде произведения многочленов выше нулевой степени, т.е. f(x) = g(x)×h(x), где cm g(x) < cm f(x) & cm g(x) ¹ 0, cm h(x) < cm f(x) &cm h(x) ¹ 0.
Определение 2. Многочлен f(x)ÎP[x] называется неприводимым над полем P, если:
1. cm f(x) > 0,
2. f(x) не разлагается в произведение многочленов меньшей степени.
Пример 1. Многочлен f(x)=x2 + 1 = (x - i)(x + i) приводим над полем С и неприводим над полем R и Q.
Многочлен h(x) = x2 - 5x + 6 = (x - 3)(x - 2) приводим над Q, R и С.
Замечание 1. Многочлены нулевой степени не входят в класс приводимых и неприводимых многочленов, а образуют свой класс, т.е. если множество натуральных чисел мы разбили на три класса:
1. единица;
2. простые числа;
3. составные числа,
то и множество Р[х] разбивается на три класса:
1. многочлены нулевой степени (аiÎР);
2. приводимые многочлены;
3. неприводимые многочлены.
Замечание 2. Приводимость многочленов зависит от поля Р. (смотри прим. 1)
Также как в кольце Z, в кольце Р[х] можно доказать аналог основной теоремы арифметики.
Теорема "f(x) ¹ 0, f(x)ÎP[x], cm f(x)>0 разлагается в произведение неприводимых многочленов единственным способом, с точностью до порядка следования многочленов нулевой степени.
Доказать самостоятельно теорему и следствие из неё.
Следствие. Если f(x) = c1p1a1(x) p2a2(x)×...× pkak(x),
g(x) = c2p1b1(x) p2b2(x)×...×psbs(x), то
(f, g) = cp1g1(x) p2g2(x)×...×pmgm(x), где gi = min(ai, bi)
[f, g] = c3p1dl(x) p2d2(x)×...×pndn(x), где di = mах(ai, bi)
Покажем, что задача о разложении многочлена на линейные множители (многочлены первой степени) сводится к задаче нахождения корней многочлена f(x) в поле Р.
Пусть f(x)=anxn + an-1xn-1 +...+ a1x + a0 и aÎР. Подставим вместо х в f(x) a. Получим, f(a)=anan + an-1an-1+...+a1a+a0 = cÎP. Элемент (с) называют значением многочлена f(x) при х = a и записывают: f(a) = c.
Определение 3. Элемент aÎР называют корнем многочлена f(x), если f(a)=0.
Ответ на вопрос о существовании корней многочлена f(x) над полями C, R и Q даёт основная теорема алгебры.
Теорема 1. 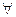 f(x) Î C[x], ст f(x) > 1 имеет хотя бы один корень.
f(x) Î C[x], ст f(x) > 1 имеет хотя бы один корень.
Опираясь на эту теорему и определение понятия корня многочлена, можно доказать теорему 2.
Теорема 2. f (a) = 0 Û f(x)/(x - a).
 2015-02-27
2015-02-27 13962
13962







