Существование первообразной для аналитической функций. Формула Ньютона- Лейбница

В этом пункте мы покажем, что формула Ньютона – Лейбница для вычисления определенных интегралов от действительных функций может быть при некоторых предположениях применена и в случае функции комплексной переменной. Предварительно сформулируем теорему для аналитической функции.

Теорема.26.3. Всякая аналитическая в односвязной области D функция f(z) имеет в этой области первообразную функцию F(z): 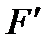(z)=f(z.)

Следующие две теоремы предлагается доказать самостоятельно.

Теорема.26.4. Если F(z) аналитическая и f(z)=0 в некоторый области Д₁, то в этой области f(z)= const.

Теорема.26.5. Любые две первообразные для одной аналитической функции отличается на константу.

Неопределенным интегралом от аналитической функций F(z) называется совокупность всех первообразных от неё,и обозначается: .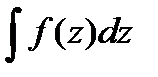

Из теоремы 26.3 и 26.5 следует, что 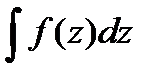= 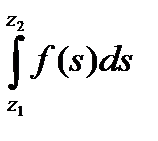+c

Теорема 26.6 Если f(z) аналитична в односвязной области D и Z₁ Z₂-любые две точки из D, то справедлива формула Ньютона-Лейбница

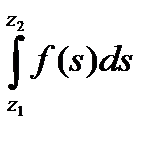=F(z₂)-F(z₁),

где F(z)-любая первообразная для f(z), а слева стоит интеграл от f(z) по любой кривой соедениящей точки Z₁ Z₂.

Доказательство. Функция F(z)= 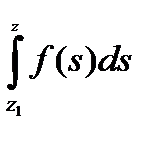+С

является первообразной для f (z). Находим F(z₁)=С_h, F(z₂)= 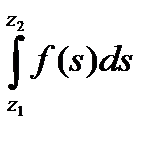+C= 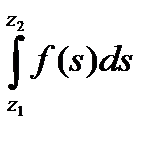+F(z₁)

Отсюда 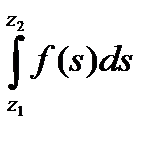=F(Z₂)-F(Z₁)

Пример.26.5. Вычислить интеграл I= 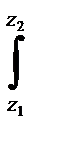sinzdz по любой кривой соединяющей точки Z₁=1 Z₂=i

Решение. Так как sinz аналитическая в односвязной области функция, то применима формула Ньютона-Лейбница

I= 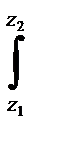sinzdz =-cosz| 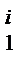=-cosi+cos1=cos1-ch1