Пусть 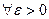
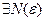 (не зависящее от
(не зависящее от 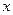 ):
): 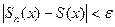
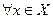 начиная с номера
начиная с номера 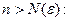 (здесь
(здесь 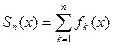 ). Тогда говорят, что функциональный ряд (1) сходится к
). Тогда говорят, что функциональный ряд (1) сходится к 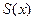
Кратко записывают: 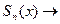
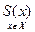 .
.
Теорема 1. (критерий Коши равномерной сходимости).
Ряд 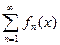 сходится на
сходится на 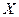 равномерно к
равномерно к 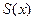
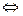
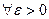
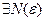 (не зависящее от
(не зависящее от 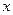 ):
):
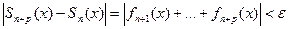 (
(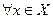 ) для
) для 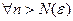 ,
, 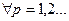
БИЛЕТ 33.
Теорема 1 (признак Вейерштрасса).
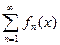 (1),
(1), 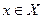 . Пусть существует сходящийся числовой ряд
. Пусть существует сходящийся числовой ряд 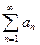 (А) и
(А) и
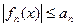
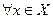
Тогда функциональный ряд (1) сходится на 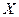 равномерно.
равномерно.
Теорема 2 (признак Абеля-Дирихле равномерной сходимости).
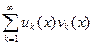 .
.
Пусть:
1). 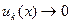 при
при 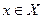 ,
, 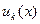 не возрастает.
не возрастает.
2). 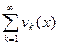
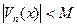
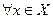 равномерно огр. на
равномерно огр. на 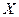 .
.
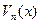 =
= 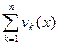
Тогда ряд 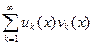 сходится равномерно на
сходится равномерно на 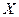 .
.
Теорема 3 (признак Дини).
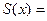
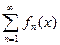
1). 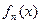 непрерывны на
непрерывны на 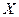
2). 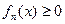 на
на 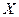
3). 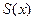 непрерывна на
непрерывна на 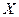 .
.
Тогда ряд сходится равномерно на 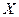 .
.
БИЛЕТ 34.
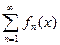 (1)
(1)
Теорема 1 (о непрерывности суммы функционального ряда).
Пусть:
1). 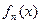 определена в
определена в 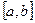 ,
, 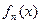 непрерывна в точке
непрерывна в точке 
2). Ряд (1) сходится равномерно в 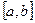 .
.
Тогда сумма функционального ряда: 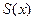 непрерывна в точке
непрерывна в точке 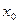 . Если же
. Если же 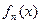 непрерывна
непрерывна
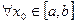 , то
, то 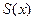 непрерывна на
непрерывна на 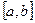
БИЛЕТ 35.
Теорема (о почленном интегрировании).
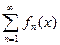 .
.
Пусть 1) 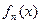 - непрерывны на
- непрерывны на 
2) Ряд сходится равномерно на  .
.
|
|
|
Тогда 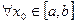 :
: 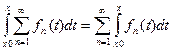 .
.
БИЛЕТ 36.
Теорема (о почленном дифференцировании).
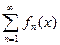 (1)
(1) 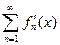 (1’)
(1’)
Пусть: 1) 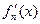 непрерывна на
непрерывна на 
2) Ряд 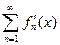 сходится равномерно на
сходится равномерно на  .
.
3) 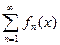 сходится на
сходится на  .
.
Тогда: 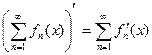 на
на  .
.
БИЛЕТ 37.
Определение: Ряд вида 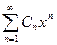 называется степенным рядом,
называется степенным рядом, 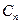 - некоторые числа, называемые коэффициентами степенного ряда.
- некоторые числа, называемые коэффициентами степенного ряда.
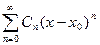 - обобщенный степенной ряд.
- обобщенный степенной ряд.
Теорема (Абеля). 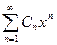 (1). Пусть ряд (1) сходится при
(1). Пусть ряд (1) сходится при 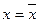 . Тогда он сходится
. Тогда он сходится 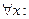
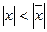 . Пусть ряд (1) расходится при
. Пусть ряд (1) расходится при  . Тогда ряд расходится
. Тогда ряд расходится 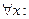
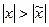 .
.
Теорема (о структуре области сходимости степенного ряда).
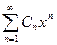 .
. 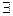 единственное число
единственное число 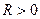 (или
(или 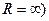 : степенной ряд сходится при
: степенной ряд сходится при 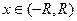 и расходится при
и расходится при 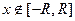 . Если
. Если 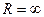 , то степенной ряд сходится всюду.
, то степенной ряд сходится всюду.
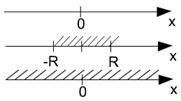 Области сходимости:
Области сходимости:
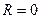
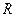
дположим, ряд сходится в точке нателе Ряд сходится.
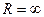
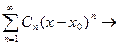
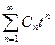 где
где 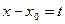
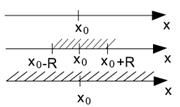
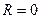
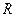
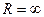
Нельзя определенно сказать что-либо о точках 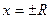 - может быть и сходимость и расходимость.
- может быть и сходимость и расходимость.
БИЛЕТ 38.
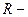 радиус сходимости степенного ряда
радиус сходимости степенного ряда 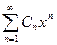
Теорема: Пусть ограниченное число 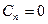 . Тогда:
. Тогда:
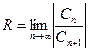 (1),
(1), 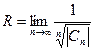 (2)
(2)
БИЛЕТ 39.
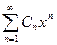 (1)
(1)
Теорема 1. Пусть 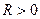 . Тогда степенной ряд (1) сходится равномерно в
. Тогда степенной ряд (1) сходится равномерно в 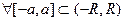 .
.
Теорема 2 (о непрерывности суммы степенного ряда).
Пусть 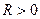 . Тогда
. Тогда 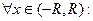 сумма степенного ряда непрерывна.
сумма степенного ряда непрерывна.
БИЛЕТ 40.
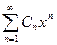 (1)
(1)
Теорема 1. Пусть 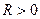 . Тогда
. Тогда 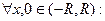
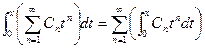 . Более того, радиус сходимости ряда, полученного после почленного интегрирования, не изменится
. Более того, радиус сходимости ряда, полученного после почленного интегрирования, не изменится 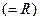 .
.
Теорема 2. Пусть 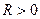 . Тогда
. Тогда 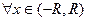 степенной ряд можно дифференцировать почленной в точке
степенной ряд можно дифференцировать почленной в точке 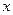 . Более того, ряд из производных имеет тот же радиус сходимости, что и исходный.
. Более того, ряд из производных имеет тот же радиус сходимости, что и исходный.
Теорема (о почленном дифференцировании функционального ряда).
Напоминание:
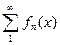 : 1)
: 1) 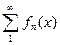 сходится 2)
сходится 2) 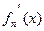 непрерывны. 3).
непрерывны. 3). 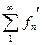 сход. равномерно в
сход. равномерно в 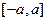 .
.
Все эти условия выполнены 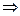 можно почленно дифференцировать степенной ряд в
можно почленно дифференцировать степенной ряд в 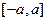
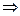 и в точке
и в точке 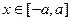 . Более того, получили, что
. Более того, получили, что 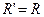 .
.
|
|
|
Следствие: степенной ряд можно почленно интегрировать и дифференцировать сколько угодно раз в области (интервале) сходимости 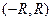 . При этом
. При этом 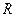 не изменяется.
не изменяется.
БИЛЕТ 41.
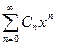 (1).
(1).
Определение: Говорят, что функция  может быть разложена в степенной ряд в
может быть разложена в степенной ряд в 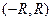 , если
, если 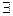 степенной ряд вида (1), сходящийся к
степенной ряд вида (1), сходящийся к  в
в 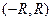 .
.
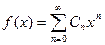 .
.
Утверждение 1. Пусть  может быть разложена в степенной ряд в
может быть разложена в степенной ряд в 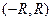 . Тогда
. Тогда 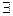 производные всех порядков у функции
производные всех порядков у функции  в
в 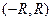 .
.
Утверждение 2. Разложение функции в степенной ряд единственно.
Замечание: 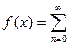
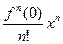 (**). (
(**). (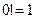 ).
).
Определение: ряд в правой части равенства (**) называется рядом Тейлора для функции 
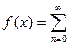
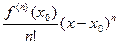 .
.
БИЛЕТ 42.
Теорема 1. (о необходимом и достаточном условиях разложимости в ряд Тейлора).
Пусть 1) функция  имеет производные
имеет производные 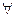 порядка в
порядка в 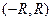 .
.
2) остаточный член формулы Тейлора 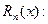
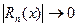 при
при 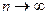
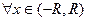
Тогда  может быть разложена в ряд Тейлора вида
может быть разложена в ряд Тейлора вида 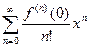 (**) в
(**) в 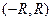 .
.
Теорема 2. (о достаточных условиях разложимости функции в ряд Тейлора).
Пусть 1) 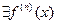
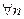
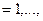 .
. 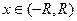 2).
2). 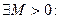
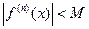
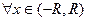
Тогда функция  может быть разложена в ряд Тейлора в
может быть разложена в ряд Тейлора в 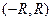 .
.
БИЛЕТ 43.
1). 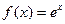
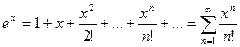
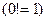
2) 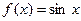
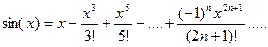
3). 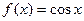
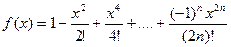
4). 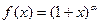 ,
, 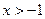 ,
, 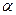 - ненатуральное число.
- ненатуральное число.
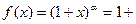
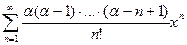
5). 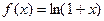
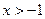
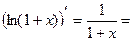
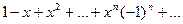
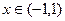
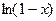
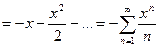 ,
, 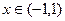
6) 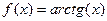
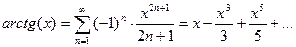
БИЛЕТ 44.
Определение 1. Обозначим через 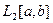 множество функций, интегрируемых с квадратом на
множество функций, интегрируемых с квадратом на  .
. 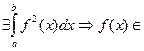
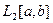 .
.
Определение 2. 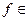
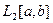 ,
, 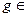
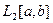
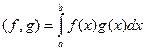 - скалярное произведение.
- скалярное произведение. 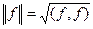 - норма функции
- норма функции  .
.
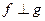 , если
, если 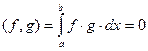 .
.
Определение 3. 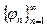 в
в 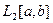 . Говорят, что система
. Говорят, что система 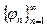 является ортогональной системой, если
является ортогональной системой, если 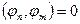 при
при 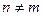 . ОС- ортогональная система.
. ОС- ортогональная система.
Определение 4. ОС 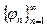 называется ортонормированной системой (ОНС), если
называется ортонормированной системой (ОНС), если 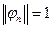 . Нормировать ОС:
. Нормировать ОС: 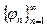
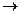
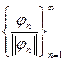 .
.
БИЛЕТ 45.

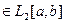 .
. 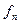
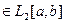 .
. 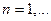
Определение: Говорят, что 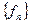 сходится в среднем к
сходится в среднем к  в
в 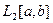 , если
, если
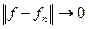 при
при 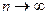 . (
. (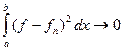 при
при 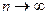 ).
).
Утверждение. Пусть 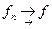 на отрезке
на отрезке  . Тогда
. Тогда 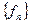 сходится к
сходится к  в среднем на отрезке
в среднем на отрезке
 .
.
БИЛЕТ 46.
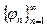 - ОНС в
- ОНС в 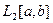 .
. 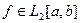 .
.
Пусть 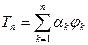 . Приближаем функцию
. Приближаем функцию  функциями
функциями 
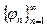 - ОНС в
- ОНС в 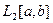 .
. 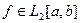 .
.
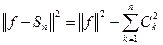 (тождество Бесселя).
(тождество Бесселя).
Минимальное свойство коэффициентов Фурье:
Если в качестве 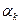 взять коэффициенты Фурье
взять коэффициенты Фурье 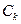 , то величина
, то величина 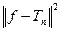 становится минимально возможной. (
становится минимально возможной. (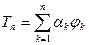 )
)
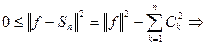
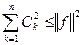 - неравенство Бесселя.
- неравенство Бесселя.
БИЛЕТ 47.
Определение:
ОНС 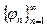 называется замкнутой системой в
называется замкнутой системой в 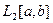 , если
, если 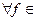
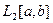 .
.
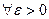
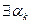 ,
, 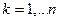
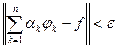 .
.
Утверждение 1. Пусть 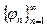 - замкнутая ОНС в
- замкнутая ОНС в 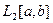 . Тогда неравенство Бесселя переходит в равенство:
. Тогда неравенство Бесселя переходит в равенство: 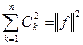 (равенство Парсеваля)
(равенство Парсеваля)
Утверждение 2. Пусть ОНС 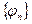 замкнута в
замкнута в 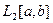 . Тогда ряд Фурье функции
. Тогда ряд Фурье функции  сходится в среднем к
сходится в среднем к  в
в 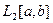 .
.
БИЛЕТ 48.
Определение: ОНС 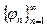 называется полной в
называется полной в 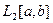 , если не существует
, если не существует 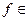
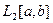 , такой что
, такой что 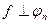 ,
, 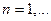
Утверждение 1: Пусть 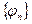 - замкнутая. Тогда
- замкнутая. Тогда 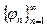 - полная ОНС.
- полная ОНС.
Утверждение 2: Пусть 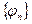 - полная (тем более замкнутая) ОНС в
- полная (тем более замкнутая) ОНС в 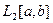 . Тогда 2 различные функции
. Тогда 2 различные функции 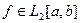 ,
, 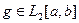 не могут иметь совпадающих рядов Фурье.
не могут иметь совпадающих рядов Фурье.
БИЛЕТ 49.
Тригонометрическая система функций:
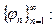
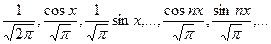 (*).
(*).
Было доказано:
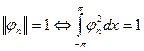 .
.
Теорема: Тригонометрическая система функций (*) является ОНС в 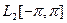
БИЛЕТ 50.
Определение 1. Говорят, что функция  с
с 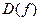 имеет период
имеет период 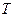 , если выполнено:
, если выполнено:
1) 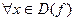
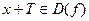 .
.
2) 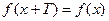 .
.
Определение 2. Ряд вида 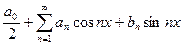 называется тригонометрическим рядом Фурье.
называется тригонометрическим рядом Фурье. 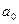 ,
, 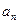 ,
, 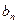 ,
, 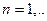 - коэффициенты Фурье.
- коэффициенты Фурье.
Теорема 1. Пусть  имеет
имеет 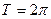 ,
, 
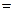
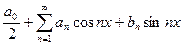 (*). Пусть ряд сходится равномерно на всей оси. Тогда:
(*). Пусть ряд сходится равномерно на всей оси. Тогда: 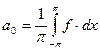 ,
, 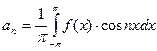 ,
,
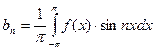 ,
, 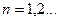
БИЛЕТ 51.
Определение: Функция  называется кусочно-монотонной на
называется кусочно-монотонной на  , если можно разбить множество
, если можно разбить множество  на отрезки
на отрезки 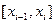 точками
точками 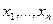 так, что на каждом из отрезков
так, что на каждом из отрезков 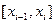 функция
функция  будет являться монотонной.
будет являться монотонной.
Пример: 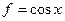 - кусочно-монотонная на
- кусочно-монотонная на 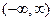 .
.
Теорема 1. (Дирихле о поточечной сходимости ряда Фурье).
Пусть  имеет
имеет 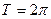 . Пусть также
. Пусть также  кусочно-монотонна в
кусочно-монотонна в 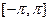 , ограничена. Тогда ряд Фурье
, ограничена. Тогда ряд Фурье 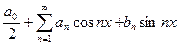 для функции
для функции  (здесь
(здесь 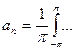 ,
, 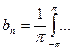 ) сходится к
) сходится к 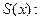
1) 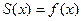 в точках непрерывности
в точках непрерывности  .
.
2). 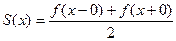 в точках разрыва функции
в точках разрыва функции  .
.
Теорема 2. (о равномерной сходимости).
Пусть  имеет
имеет 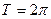 ,
,  непрерывна в
непрерывна в 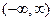 . Тогда ряд Фурье для
. Тогда ряд Фурье для  сходится к
сходится к 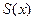 , причем равномерно (
, причем равномерно (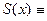
 ).
).
Теорема 3. (признак равномерной сходимости ряда Фурье). Пусть сходится ряд 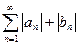 . Тогда ряд Фурье
. Тогда ряд Фурье 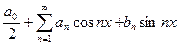 сходится равномерно по всей оси
сходится равномерно по всей оси 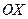 .
.
БИЛЕТ 52.
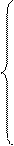
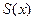
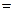
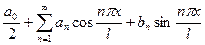 ,
,
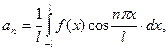 (
(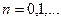 ) Ряд Фурье для функции с произвольным периодом.
) Ряд Фурье для функции с произвольным периодом.
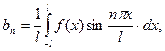 (
(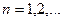 )
)
БИЛЕТ 53.

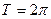
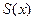
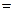
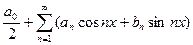
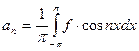
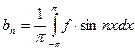 ,
,
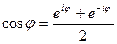 ,
, 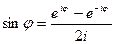
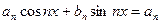
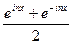 +
+ 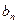
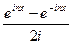 =
= 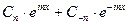 , где
, где 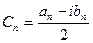 .
.
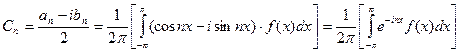 ,
, 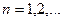
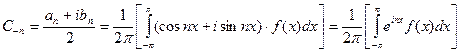 ,
, 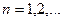

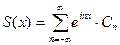
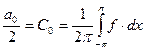 ,
,
где 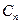 =
= 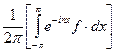 ,
, 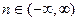 ,
, 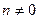 .
.
 2015-05-05
2015-05-05 1430
1430







