2015-05-26
1576
Как известно, любая электрическая цепь состоит или может быть представлена в виде двухполюсников. Пассивный двухполюсник однозначно определяется значениями тока и напряжения на входе или их отношением.
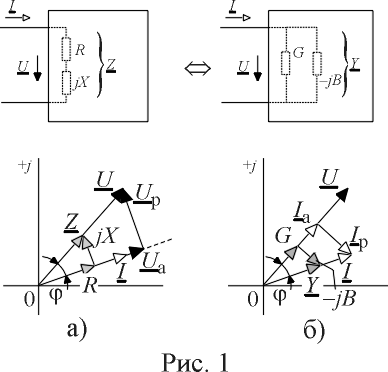Пусть через некоторый двухполюсник протекает переменный ток и существует падение напряжения. Изобразим ток и напряжение на входе двухполюсника векторами на комплексной плоскости I и U (рис. 1).
Проектируя вектор U на направление вектора I (рис. 1 а)), получим вектор, модуль которого равен U а= U cosj, где j - разность начальных фаз напряжения и тока на входе двухполюсника, причем, направление вектора U а совпадает с направлением вектора тока, поэтому его запись в показательной форме будет иметь вид
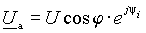 , | (1) |
где y i - начальная фаза тока на входе двухполюсника.
Перпендикуляр, опущенный из конца вектора U на направление вектора тока, имеет длину U sinj и может рассматриваться как некоторый вектор U р, сумма которого с вектором U а равна U (рис. 1 а)). Его также можно записать в показательной форме в виде
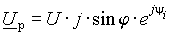 . | (2) |
Оператор поворота j в выражении (2) учитывает перпендикулярное положение вектора U р по отношению к I и условие U а + U р = U.
Так как по построению векторы U а и U р в сумме равны U, то из выражений (1) и (2) вектор напряжения на входе двухполюсника можно представить как
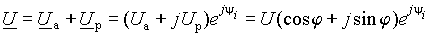 . | (3) |
Разделим выражение (3) на модуль вектора тока
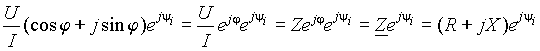 . | (4) |
Выражение (4) соответствует представлению на комплексной плоскости вектора Z, равного комплексному сопротивлению двухполюсника и развернутого относительно вещественной оси на угол y i. При этом вектор Z e jj e jy i=Zej (y u- y i+ y i)= Ze jy u образует с вещественной осью комплексной плоскости угол y u, т.е. оказывается совпадающим по направлению с вектором U.
Сравнивая вещественные и мнимые части выражений (3) и (4), можно представить модули составляющих вектора U в виде
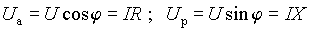 , | (5) |
т.е. модуль составляющей U а, называемой активной или резистивной составляющей напряжения на входе двухполюсника, представляет собой падение напряжения на резистивной составляющей его комплексного сопротивления при токе I. Аналогично, модуль вектора U р, называемого реактивной составляющей входного напряжения, является падением напряжения на реактивной составляющей комплексного сопротивления.
Рассмотренным соотношениям величин соответствует представление двухполюсника последовательным соединением резистора R и реактивного сопротивления X, представленным на рис. 1 а).
Таким образом, вектор падения напряжения на входе двухполюсника может быть представлен двумя составляющими, одна из которых является его проекцией на направление вектора входного тока и называется активной (резистивной) составляющей или активным падением напряжения. Активная составляющая соответствует падению напряжения на резистивном сопротивлении последовательной эквивалентной схемы двухполюсника. Вторая составляющая перпендикулярна вектору тока и соответствует падению напряжения на реактивном сопротивлении последовательной эквивалентной схемы.
Прямоугольные треугольники UU а U р и ZRX (рис. 1 а)) подобны и называются соответственно треугольниками напряжений и сопротивлений.
ЗАДАЧА 1
Спроектируем теперь вектор тока I на направление вектора падения напряжения U (рис. 1 б)). Длина проекции будет равна I а= I cosj, а длина проектирующего перпендикуляра - I р= I sinj. Представим эти отрезки векторами с учетом того, что I а совпадает с направлением вектора падения напряжения на входе двухполюсника, а в сумме эти два вектора должны быть равны I. Тогда в показательной форме -
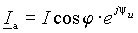 | (6) |
 | (7) |
Множитель - j является оператором поворота отрезка I р на 90° в направлении отставания, чтобы обеспечивалось условие I а + I р = I.
Представим теперь вектор тока через полученные составляющие
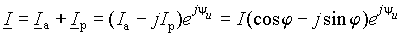 . | (8) |
Разделим выражение (8) на модуль вектора U -
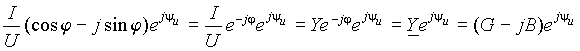 . | (9) |
Таким образом, из прямоугольного треугольника, составленного из векторов I а, I р и I и описанного выражением (8), делением на постоянную величину U всех его сторон мы получили подобный треугольник, описываемый выражением (9). Стороны нового треугольника имеют размерность проводимости и связаны с составляющими вектора тока законом Ома
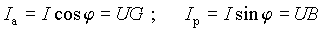 . | (10) |
Следовательно, активную и реактивную составляющую вектора тока можно представить, в виде токов, протекающих через активную (резистивную) проводимость G и реактивную проводимость B эквивалентной параллельной схемы двухполюсника (рис. 1 б)).
Прямоугольные треугольники II а I р и YGB (рис. 1 б)) подобны и называются соответственно треугольниками токов и проводимостей. Очевидно, что треугольники токов и проводимостей подобны треугольникам напряжений и сопротивлений, т.к. имеют одинаковые углы.
Обобщая понятия составляющих векторов тока и напряжения на входе двухполюсника, можно сделать следующие выводы:
- активная (резистивная) и реактивная составляющие вектора напряжения на входе двухполюсника соответствуют падениям напряжения на резистивном и реактивном сопротивлениях последовательной эквивалентной схемы (схемы R-X);
- активная (резистивная) и реактивная составляющие вектора тока на входе двухполюсника соответствуют токам, протекающим через резистивную и реактивную проводимости параллельной эквивалентной схемы (схемы G-B);
- понятиями активной и реактивной составляющих тока и напряжения можно пользоваться, не связывая их с какой-либо эквивалентной схемой двухполюсника, т.к. из подобия треугольников напряжений, токов, сопротивлений и проводимостей следует взаимно однозначная связь этих величин.
Последовательное и параллельное соединения
Эквивалентные параметры
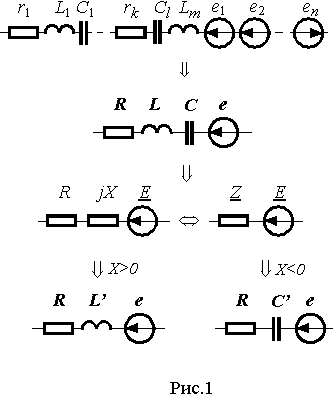В последовательное соединение в цепях переменного тока кроме резисторов могут входить реактивные элементы - индуктивности и емкости.
Пользуясь понятием потенциала, падение напряжения на последовательном соединении (рис. 1) можно представить суммой падений напряжений на отдельных элементах
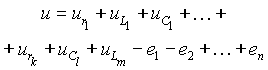 | (1) |
Последовательное соединение не содержит узлов, поэтому по всем его элементам протекает одинаковый ток. Пусть этот ток равен i = Im sinw t, тогда, с учетом выражений для падения напряжения на реактивных элементах, выражение (1) преобразуется к виду
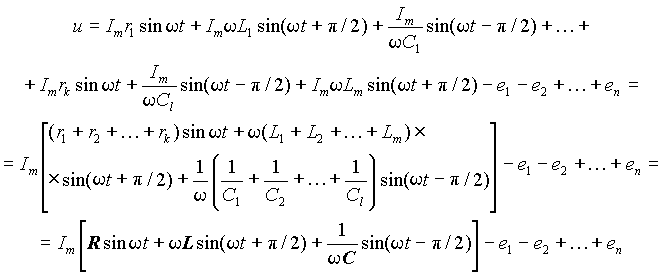 | (2) |
Таким образом, в последовательном соединении все резисторы, индуктивности и емкости можно заменить эквивалентными элементами R, L и C, причем
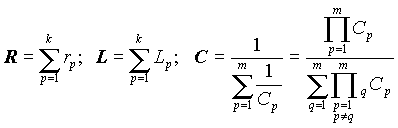 . | (3) |
Из выражений (3) следует, что эквивалентные сопротивление и индуктивность больше наибольшего из значений параметров элементов, входящих в соединение, а эквивалентная емкость - меньше наименьшего из значений. Иначе говоря, последовательное подключение в цепь сопротивления или индуктивности увеличивает их эквивалентные значения, а последовательное подключение емкости - уменьшает.
Рассмотренные выше преобразования последовательного соединения не затрагивали входящих в него источников ЭДС. Это связано с тем, что во временной области ЭДС являются синусоидальными функциями с различными начальными фазами. Поэтому их преобразование лучше провести, перейдя к изображениям комплексными числами и векторами.
Как известно, операции суммирования в области оригиналов соответствует суммирование и в области изображений. Отсюда
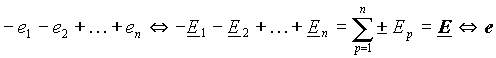 , | (4) |
где E и e - изображение и оригинал эквивалентного источника ЭДС, т.е. любое количество последовательно соединенных источников ЭДС можно заменить одним эквивалентным, значение ЭДС которого равно алгебраической сумме ЭДС, входящих в соединение.
После того, как резисторы, индуктивности, емкости и ЭДС заменены эквивалентными параметрами и элементами можно определить комплексное сопротивление пассивных элементов
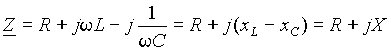 . | (5) |
Мнимая часть комплексного сопротивления Z может быть положительной или отрицательной в зависимости от того какое сопротивление больше, индуктивное xL или емкостное xC. При положительном значении реактивной составляющей комплексного сопротивления X, соединение L - C можно представить индуктивностью L', реактивное сопротивление которой xL' равно X. Отсюда значение эквивалентной индуктивности
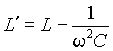 , | (6) |
где L и C - значения эквивалентной индуктивности и емкости, определенные из выражений (3). В случае X <0, реактивные элементы, входящие в последовательное соединение можно представить эквивалентной емкостью
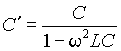 . | (7) |
Таким образом, в случае заданного значения частоты последовательное соединение можно представить последовательным соединением резистора, реактивного элемента и источника ЭДС, параметры которых определяются по выражениям (3), (4), (6) и (7). Резистор, реактивный элемент и источник ЭДС являются минимальным набором элементов, с помощью которых можно представить последовательное соединение. При наличии в цепи реактивных элементов обоих типов (индуктивности и емкости) в минимальном наборе элементов (минимальной эквивалентной схеме) будет присутствовать только один из них.
При отсутствии каких-либо элементов в исходной схеме, например резисторов или источников ЭДС, будут отсутствовать и соответствующие компоненты эквивалентного представления.
ЗАДАЧА 1
Перейдем теперь к рассмотрению параллельного соединения элементов цепей переменного тока.
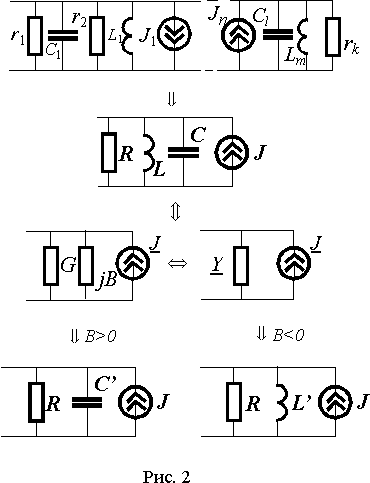
В параллельное соединение (рис. 2) могут входить резистивные и реактивные элементы, а также источники тока.
Источники ЭДС не могут соединяться параллельно, т.к., если два источника e 1 и e 2 подключены к узлам a и b, то uab = e 1 и uab = e 2, что возможно только при e 1= e 2.
Общий ток, протекающий через соединение в целом, представляет собой сумму токов, протекающих через отдельные элементы. Поэтому можно написать
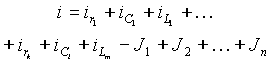 | (8) |
Все элементы соединения подключены к двум узлам, разность потенциалов которых является падением напряжения на каждом элементе. Пусть это напряжение u равно Um sinw t. Тогда
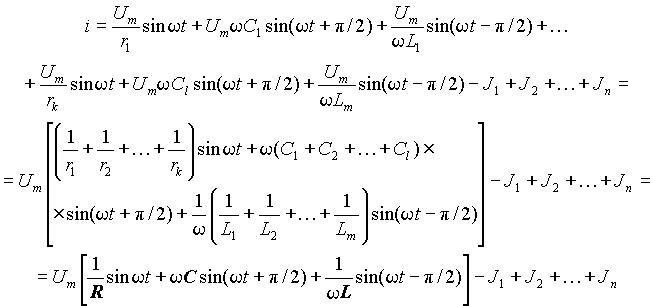 | (9) |
Из выражения (9) следует, что в параллельном соединении все резисторы, индуктивности и емкости можно заменить эквивалентными элементамиR, L и C, значения которых определяются выражениями
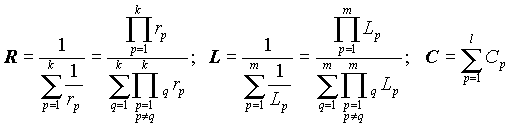 | (10) |
Из этих выражений следует, что параллельное подключение резистора или индуктивности уменьшает их эквивалентные значения, а параллельное подключение емкости - увеличивает эквивалентную емкость. Эквивалентное сопротивление R и индуктивность L всегда меньше наименьшего из параметров элементов, образующих соединение. В то время как эквивалентная емкость C - больше, чем самая большая емкость параллельного соединения.
Для определения тока эквивалентного источника воспользуемся представлением токов комплексными числами аналогично тому, как это было сделано для ЭДС последовательного соединения
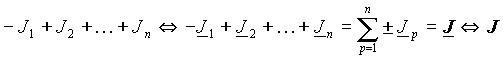 | (11) |
т.е. путем перехода к изображениям в виде комплексных чисел, а зетам обратного перехода во временную область можно получить параметры эквивалентного источника тока J, заменяющего собой все источники входящие в соединение.
Комплексная проводимость соединения может быть выражена через эквивалентные параметры следующим образом
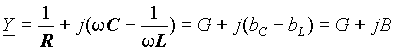 . | (12) |
В зависимости от соотношения значений емкостной и индуктивной проводимостей bL и bC, реактивная составляющая комплексной проводимости B может быть положительной или отрицательной. В первом случае, параллельное соединение L - C можно представить емкостью C ', проводимость которой равна B. Во втором случае, реактивную проводимость можно создать эквивалентной индуктивностью L '. Значения L ' и C ' можно определить как
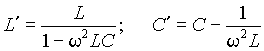 . | (13) |
Следовательно, при заданной частоте параллельное соединение, также как и последовательное, можно представить минимальным набором элементов, включающим параллельно соединенные резистор, реактивный элемент и источник тока. Тип реактивного элемента (индуктивность или емкость) определяется знаком эквивалентной реактивной проводимости.
Следует особо подчеркнуть, что выражения (3) и (10) не содержат частоты w в качестве параметра. Поэтому они справедливы всегда и применяются как для расчетов, так и при операциях с реальными объектами. Например, две соединенные последовательно катушки индуктивности в 40 и 60 мГн можно заменить одной с индуктивностью в 100 мГн. В то же время, переход к одному реактивному элементу (выражения (6), (7) и (13)) возможен только для конкретного значения частоты и применяется чаще всего в расчетных задачах.
