Анализ цепи переменного тока с активно-ёмкостным сопротивлением

В реальных цепях переменного тока с емкостью всегда имеется активное сопротивление (сопротивление проводов, активные потери в конденсаторе и т. д.). Поэтому реальную цепь с емкостью следует рассматривать состоящей из последовательно соединенных активного сопротивления R и конденсатора С (рис. 1-14, а).

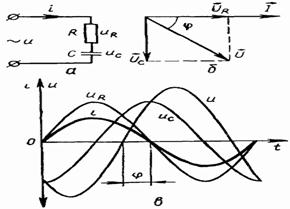
Рис. 1-14

Для такой цепи уравнение электрического равновесия в соответствии со вторым законом Кирхгофа можно записать так:

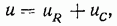
т. е. приложенное напряжение и уравновешивается суммой напряжений на элементах цепи R и С соответственно.

Если установившийся ток i в цепи принять равным напряжения на элементах R и С этой цепи будут равны

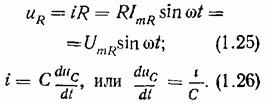
Интегрируя уравнение (1.26), получим:

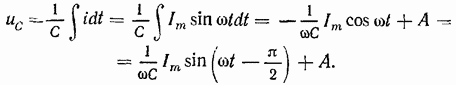
Здесь A = 0 (постоянная интегрирования). При синусоидальном токе напряжение на конденсаторе также синусоидально. При 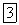имеем:

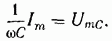
Окончательно:

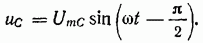
Подставим соотношения (1.26) и (1.27) в условие электрического равновесия (1.23):

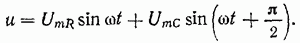
Следовательно, приложенное напряжение и является также синусоидальным, поэтому допущение (1.24) о синусоидальной форме тока является правильным.

Из векторной диаграммы (рис. 1-14, б) следует, что в рассматриваемой цепи ток опережает по фазе приложенное напряжение, но не на , как в случае чистой емкости, а на некоторый угол причем и при заданной емкости С зависит от значения активного сопротивления R (угол уменьшается с увеличением R).

Таким образом, для рассматриваемой цепи приложенное напряжение можно представить в виде

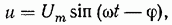
где (из векторной диаграммы).

Временные диаграммы тока и напряжений в цепи с R и С представлены на рисунке 1-14, в.

На векторной диаграмме (см. рис. 1-14, б) векторы образуют треугольник напряжений, из которого следует:

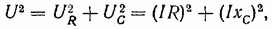
откуда

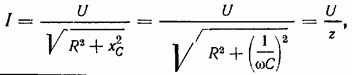
где полное сопротивление цепи с R и С, а выражение

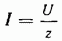
представляет собой закон Ома для активно-индуктивной цепи.

Разделив стороны треугольника напряжений на значение тока в цепи получим треугольник сопротивлений, из которого найдем угол из соотношения

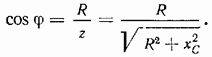
Для выяснения закона изменения мощности в цепи с R и С представим ток и напряжение в следующем виде:

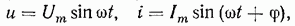
тогда мгновенное значение мощности равно

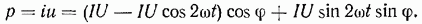
Как видно, мгновенное значение мощности имеет две составляющие: активную и реактивную (емкостную) , причем обе составляющие зависят от угла сдвига между током и напряжением. Так, в случае цепь становится чисто активной (см. рис. 1-6):

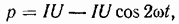
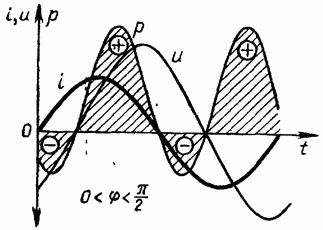
Рис. 1-15

а в случае чисто емкостной (см. рис. 1-13):

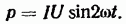
Временную диаграмму мгновенной мощности можно построить, перемножая ординаты соответствующих диаграмм тока и напряжения для каждого момента времени (рис. 1-15). Когда средняя за период мощность (активная) не равна нулю; электрическая энергия при этом безвозвратно расходуется в активном сопротивлении

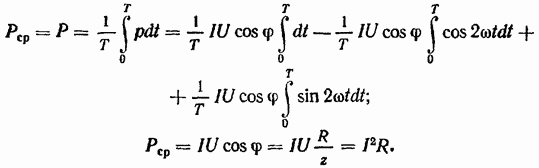
Среднее же значение реактивной (емкостной) составляющей мощности равно нулю:

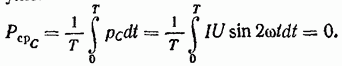
Таким образом, в случае цепи переменного тока с R и С изменение значений R и С приводит к изменениямсдвига фаз в пределах