Исправления ошибок корректирующим кодом

зона, окружающая каждую разрешенную кодовую комбинацию.

При декодировании кодовые комбинации, попадающие в эту зону, отождествляются с разрешенной. Трехкратная ошибка в В_1р(отмечено стрелкой) переводит эту, комбинацию в зону В_2р и при декодировании будет решено, что передавалась В, (ошибки не исправлены).

Пример 18.1. Кодовое расстояние корректирующего кода d_о=4. Ошибки

какой кратности данный код может обнаруживать или исправлять?

Из (18.3) и (18.4) следует, что q_o.ош <do — 1 и q_и.ош ≤(d_o -1)/2. При d_o=4

получаем: кратность обнаруживаемых ошибок q_o.ош≤ 3; кратность исправляемых

ошибок q_и.ош =1.

Пример 18.2. Чему должно быть равно кодовое расстояние do, достаточное для исправления трехкратных ошибок?

Подставляя в (18.4) значение q_и.ош =3, получаем d_o≥7.

Итак, задача получения кода с заданной корректирующей способностью сводится к задаче формирования в кодере М, разрешенных кодовых комбинаций с требуемым минимальным расстоянием d_o. Исследования показывают, что хороший корректирующий

код {кратность исправляемых ошибок q_и.ош≥5 при относительной скорости Rk≥0,5) должен иметь число информационных символов k≥40. А это накладывает технические трудности на описанную процедуру декодирования принятой кодовой комбинации со всеми

разрешенными. Это наглядно показывает приведенный ниже пример.

Пример 18.3. Определить время декодирования сравнением принятой кодовой комбинации со всеми разрешенными при k=48, если для этого используется ЭВМ, производящая 10⁷ оп./с.

Будем считать, что для сравнения принятой кодовой комбинации с одной

из разрешенных достаточно одной операции на ЭВМ. Всего необходимо провести М_a— 1 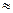2⁴⁸ сравнений, и на это потребуется время Т=2⁴⁸/7=2,8*107 с 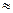325,8 суток, т. е. около 11 месяцев.

Как видно из примера 18.3, задача декодирования простым перебором и сравнением непосильна даже для современных ЭВМ (и, пожалуй, ЭВМ будущего). На практике получили распространение такие методы кодирования и декодирования, которые не требуют перебора при декодировании и имеют приемлемую сложность реализации.

Одним из наиболее часто применяемых является синдромный способ декодирования, основанный на простом правиле: для исправления ошибки необходимо знать не только факт ее существования, но и местонахождение. Под синдромом кода понимают контрольное число C(c₁, с₂...с_r), указывающее на наличие и расположение (конфигурации) ошибок в кодовой комбинации. Заметим, что в двоичном коде синдром записывается в двоичной системе

счисления, т. е. его разряды c₁, с₂...с_r принимают значения 0 или 1. Нулевой синдром указывает на то, что принятая кодовая комбинация является разрешенной, т. е. обнаруживаемых ошибок нет.

Всякому ненулевому синдрому соответствует определенное расположение ошибок.

Достаточно ли знание синдрома для исправления ошибки? В общем случае — нет. Требуется еще знать, на какой символ необходимо заменять ошибочный. Но для двоичных кодов исправление ошибки производится единственным образом — инверсией

символов (0 заменяется на 1 и 1 на 0), поэтому знание синдрома является необходимым и достаточным условием для исправления ошибок в двоичных кодах.

Таким образом, синдромное декодирование двоичных кодон сводится к вычислению тем или другим способом синдрома, по которому обнаруживаются и исправляются ошибки. Десятки предложенных до настоящего времени корректирующих кодов как раз и отличаются способами формирования проверочных символов и вычисления синдрома при декодировании.

Классификация корректирующих кодов. Исходя из основных параметров и способов кодирования и декодирования, корректирующие коды в первую очередь можно разделить нг блочные и непрерывные. Блочные коды характеризуются тем, чтo каждому знаку алфавита соответствует блок (кодовая комбинация) из и элементов. Операции кодирования и декодирования r каждом блоке производятся отдельно. Особенностью непрерывных кодов является то, что информационная последовательность не разделяется на блоки, а проверочные символы размещаются по определенному правилу между информационными. Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно указать информационные и проверочные символы. Н

неразделимых кодах такое разделение символов провести невозможно.

Разделимые коды, в свою очередь, делятся на систематические и несистематические. Систематическими называются коды, у которых сумм а по модулю два двух разрешенных кодовых комбинаций дает снова разрешенную кодовую комбинацию. Кроме того, и систематическом коде информационные символы, как правило, не изменяются при кодировании и занимают определенные заранее заданные места. Проверочные символы вычисляются как линейная комбинация информационных. Отсюда возникает и другое название систематических кодов — линейные. Для систематических кодов применяется обозначение (и, k)-код, где n — общее число символов в кодовой комбинации, k — число информационных символов. В несистематических кодах приведенные выше правила не выполняются.

Принцип построения некоторых применяемых в настоящее время корректирующих кодов приведены ниже (§ 18.3... 18.5). Схемная реализация алгоритмов кодирования и декодирования производится на основе логических элементов вычислительной техники и рассматривается в специальных курсах (телеграфия, передача данных, импульсная техника).

18.3. КОДЫ С ПОСТОЯННЫМ ВЕСОМ

Из названия кода следует, что все разрешенные кодовые комбинации такого кода имеют одинаковое число единиц. Напомним (см. §18.1), что весом называется число единиц в кодовой комбинации. Коды с постоянным весом относятся к классу блочных неразделимых кодов, так как здесь нельзя выделить информационные и проверочные символы.

Типичным примером кода с постоянным весом является семиэлементный телеграфный код # 3 (МТК-З), рекомендованный Международным консультативным комитетом по телефонии и телеграфии (МККТТ) для использования в системах с обратной связью с целью обнаружения ошибок. Вес кода равен трем, следовательно, каждая разрешенная кодовая комбинация имеет три единицы и четыре нуля. В МТК-3 из общего числа кодовых комбинаций Мo=2₇=128 разрешенными являются лишь М_a=С^З₇=35 поэтому в соответствии с (18.1) относительная скорость кода R_k== log₂35/ log₂128=0,73. Декодирование принятых кодовых комбинаций в коде с постоянным весом сводится к вычислению их веса (подсчета числа единиц). Если вес отличается от заданного, то выносится решение, что комбинация принята с ошибкой. Например, легко определить, что из трех принятых кодовых комбинаций МТК-3; 1011000, 110101, 010101, — ошибки имеются во второй, поскольку ее вес равен четырем. Этот код обнаруживает все ошибки нечетной кратности и часть ошибок четной кратности. Не обнаруживаются только так называемые ошибки смещения, сохраняющие неизменным вес комбинации. Характерным для ошибок смещения является то, что число

искаженных единиц всегда равно числу искаженных нулей, поэтому коды с постоянным весом наиболее эффективны в каналах, где вероятность ошибок смещения невелика.

18.4. КОД С ЧЕТНЫМ ЧИСЛОМ ЕДИНИЦ

Это систематический (k+ 1, k)-код, в котором операции кодирования и декодирования проводятся как проверка на четность. Кодовое расстояние для этого кода d_о = 2. При этом согласно (18.3) код всегда обнаруживает однократные ошибки. Разрешенная комбинация этого кода при любом числе информационных символов имеет всего один проверочный. Размещение проверочного символа в кодовой комбинации не имеет значения. Обычно его ставят в конце после информационных. Значение символа в проверочном разряде выбирается из условия, что общее число единиц в образованной таким образом разрешенной кодовой комбинации было четным (отсюда и название кода), т. е. чтобы сумма по модулю для всех символов кодовой комбинации равнялась нулю.

Если разряды кодовых комбинаций пронумеровать справа налево и символы в этих разрядах обозначить для безызбыточного кода a₁а₂...а_k, а для корректирующего b₁b₂...b_kb_k+1, то описанная выше процедура формирования разрешенной кодовой комбинации запишется в виде:

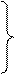b_i=a_i при i=1, 2,..., k;

b_k+1=а1 а2 ... аk,

причем c1=b₁ b₂... b_k b_k+1=0, (18.6)

где, как и раньше, знак означает суммирование по модулю два. В (18.5) первое равенство означает, что информационные символы при кодировании не изменяются, второе — описывает правило формирования проверочного символа. Уравнение (18.6) определяет синдром (контрольную сумму) этого кода как результат проверки кодовой комбинации на четкость. При любой однократной ошибке при передаче (безразлично, в информационных или проверочном символах) условие (18.6) нарушается и тем самым обнаруживается ошибка.

Пример 18.4. Необходимо передать кодом с четным числом единиц кодовую комбинацию 10110. Проверочный символ в соответствии с выражением (18.5), b_k+1=1 0 1 1 0=1. Следовательно, передаваемая кодовая комбинация будет иметь вид

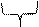101101

информационные символы проверочный символ

Пусть будет принята комбинация 101001. Контрольная сумма C1=1 0 1 0 0 1=1≠0, что свидетельствует о наличии ошибки. Нарушение четности имеет место при появлении не только однократных, но и любых ошибок нечетной кратности, что дает возможность их обнаружить. Появление четных ошибок не изменяет четности контрольной суммы (18.6), поэтому такие ошибки кодом с четным числом единиц не обнаруживаются.

К достоинствам рассмотренного кода следует отнести простоту кодирующих и декодирующих устройств, малую избыточность x_и=1/(1+k). Однако этот код имеет сравнительно низкую корректирующую способность, ограничивающую его применение.

18.5. ЦИКЛИЧЕСКИЕ КОДЫ

Циклические коды относятся к систематическим кодам. Они получили название благодаря своему свойству: циклическая перестановка символов разрешенной кодовой комбинации дает снова разрешенную кодовую комбинацию. При циклической перестановке

символы кодовой комбинации перемещаются слева направо на одну позицию, причем крайний правый символ переносится на место

крайнего левого. Например, с А₁ =101 100 циклической перестановкой получаем А₂=010110.

В теории циклических кодов все преобразования кодовых комбинаций производятся в виде математических операций над полиномами (многочленами). Для этого кодовые комбинации циклического кода представляют в форме полиномов. Так, кодовая комбинация А=а_nа_n-1... а₁а₀ при аi={1, 0} записывается в виде

А (х) =а_nхⁿ-а_n-1х^n-1 +... +а₁х+а_ох^o.

Запись полинома обычно упрощают, опуская сомножители а_i=1 и вычеркивая слагаемые, в которые входит аj=О. Например, кодовая комбинация А₁=101100 представляется полиномом А₁(х) =х⁵+х³+х², а A₂ = 010110 — полиномом А₂(х) =х⁴+х²+х.

Операции над многочленами. При формировании кодовых комбинаций циклического кода и вычислении синдрома используются такие операции, как сложение, вычитание, умножение и деление многочленов. Они выполняются по обычным арифметическим правилам, только суммирование производится как сложение по модулю два, а вычитание заменяется суммированием. Покажем выполнение этих операций на конкретных примерах ранее приведенных полиномов A₁(x) и А₂(х):

А₁(х)+А₂(х) =А₁(х) — А₂(х) =х⁵+х³+х²+х⁴+х¹+х=

=х⁵+х⁴+х³+х поскольку х²+х²=х²(1 1) =0;

А₁(х) А₂(х) = (х⁵+х³+х²) (х⁴+х²+х) =х⁹+х⁷

+х⁶+х⁷+х⁵+х⁴+х⁶+х⁴+х^з = х⁹+х⁵+х³.

А₁(х)/А₂(х) = х⁵+ х³ + х² | х⁴+ х² + х

х

x⁵ +х³+ х²

0 0 0

Формирование разрешенных кодовых комбинаций. Разрешенные кодовые комбинации цикличесокго кода обладают важным отличительным признаком: все они без остатка

делятся на полином G(x), называемый образующим, или порождающим. Из этого свойства следует весьма простой способ формирования разрешенных кодовых комбинаций — умножение комбинаций первичного кода Аi(х) на порождающий полипом G(x):

Вip(х) =Аi(х)G(х). (18.7)

В теории циклических кодов доказывается, что порождающими

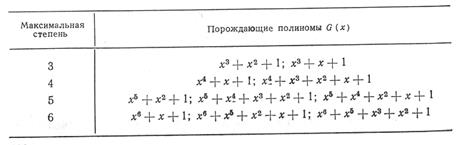
могут быть только полиномы, которые являются делителями двучлена хⁿ + l. Такие полиномы, найденные с помощью ЭВМ, сведены в обширные таблицы. Некоторые из них приведены в табл. 18.1. Следует отметить, что с увеличением максимальной степени

порождающих полиномов r резко увеличивается их количество.

Так, при r=3 имеется всего два полинома, при r=10 их уже несколько десятков.

Для формирования разрешенных кодовых комбинаций по алгоритму (18.7) может быть использован любой порождающий полином, лишь бы его максимальная степень была равна числу необходимых проверочных символов. Однако в полученной таким способом комбинации В~~(х) в явном виде не содержатся информационные символы (получаем неразделимый код), поэтому на практике используют другой способ кодирования, позволяющий представить кодовую комбинацию В_iр в виде разделенных информационных и проверочных символов:

B_ip(x) =Аi(х)х^r +R(x),

где R(x) — остаток от деления А_i(х)х^r/G(х).

В алгоритме (18.8) можно выделить три этапа формирования

разрешенных кодовых комбинаций:

1) к комбинации первичного

кода Аi дописывается справа r нулей, что эквивалентно умножению А_i(х) на х^r;

2) произведение А_i(х)х' делится на порождающий полином G(х) и определяется остаток R(х), степень которого не превышает r — 1;

3) вычисленный остаток присоединяется к

А_i (х) х^r.

Таблица 18.1. Порождающие полиномы 6(х) циклических кодов

Пример 18.5. Для кодовой комбинации А_i =1011 сформировать кодовую

комбинацию циклического кода (7, 4).

В заданном цикличеоком коде n=7, k=4, r=3 и из табл. 18.1 выберем

порождающий полином G(х)=х³+х₂+1. Проделаем необходимые операции по

получению кодовой комбинации циклического кода согласно алгоритму (18.8):

A_i(x)x^r=(x³+x+1)x³=x⁶+x⁴+x³;

A_i(x)x^r/G(x)=x⁶+x⁴+x³ | x³+x²+1

x³+x²

x⁶+x⁵+x³

X⁵+x⁴

x⁵+x⁴+x²

R(x)=x²

A_i(x)x^r+R(x)=x⁶+x⁴+x³+x²=B_ip(x)

Полученная кодовая комбинация циклического кода может быть также записана в виде B_ip =1011100, где первые четыре символа являются информационными, последние три — проверочными.

Синдром циклического кода. Для определения синдрома циклического кода достаточно поделить принятую кодовую комбинацию на порождающий полином. Остаток от деления и является синдромом. Если принятая комбинация — разрешенная, то остаток от деления будет нулевым. Ненулевой остаток свидетельствует о наличии в принятой комбинации ошибок.

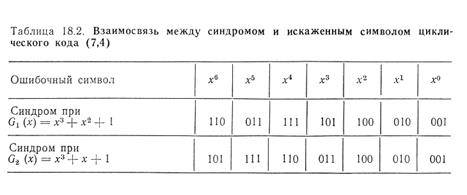
Взаимосвязь между синдромом (остатком) и ошибочным символом находится достаточно просто. Необходимо взять любую разрешенную кодовую комбинацию, ввести ошибку в определенный символ и выполнить деление на G(х). Полученный остаток

(синдром) и будет указывать на ошибку в этом символе. Для циклического кода (7,4) взаимосвязь между синдромом и ошибочным символом при различных порождающих полиномах приведена в табл. 18.2. Пользуясь этой таблицей, по синдрому можно найти

местоположение ошибки и исправить ее.

Пример 18.6. Принятая кодовая комбинация циклического кода (7,4) имеет

вид В'_ip= 1010101. Определить и исправить ошибку в В'ip если она имеется.

Порождающий полипом кода G(х) =х³+х+1.

Проводим операцию деления В'_iр(х)/G(«):

x⁶+x⁴+x²+1 | x³+x+1

x³+1

x⁶+x⁴+x³

X³+x²+1

x³+x+1

C(x)=x²+x

По табл. 18.2 находим, что синдрому (С(х) =х²+x=110 соответствует ошибочный символ х⁴. Инвертировав его, получим принятую кодовую комбинацию без ошибки В_ip=1000101.

.

Применение циклических кодов. Циклические коды просты в реализации. Все приведенные выше операции умножения, сложения и деления полиномов осуществляются на регистрах сдвига. Кроме того, эти коды обладают высокой корректирующей способностью. Можно сформировать циклический код с любым, наперед заданным значением кодового расстояния d_o. Поэтому они рекомендованы МККТТ для применения в аппаратуре передачи данных. Так, согласно Рекомендации V.41, в системах передачи данных с обратной связью следует применять код с по рождающим полиномом G(x) =х¹⁶+х¹²+х⁵+1. Можно сказать, что

в современной аппаратуре с коррекцией ошибок применяются, в

основном, циклические коды.