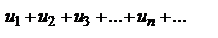Пусть имеем два ряда с положительными членами

(1) и 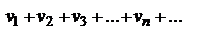(2), для которых выполняется условие: 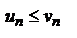. Тогда из сходимости ряда 2 следует сходимость ряда 1;

Из расходимости ряда 1 следует расходимость ряда 2.

Предельный признак сравнения.

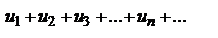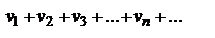Имеем два ряда (1) и (2).

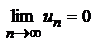. Если L существует, то оба ряда сходятся одновременно.

Пусть ряд 2 сходится, тогда по обычному признаку сравнения сходится и ряд 1.

Имеем ряд :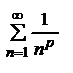

1) 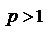ряд сходится

2) 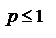ряд расходится.

Признак Даламбера.

Если в ряду с положительными членами 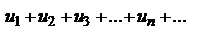отношение (n + 1)-го члена к n-му при 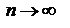имеет конечный предел l, то есть 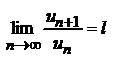, то

ряд сходится в случае ;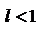

ряд расходится в случае 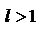;3) в случае 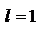ответа о сходимости или расходимости ряда теорема не дает.