2015-05-30
306
Если в ряду с положительными членами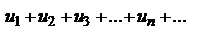 
отношение (n + 1)-го члена к n-му при 
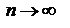имеет конечный предел l, то есть 
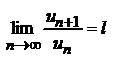, то
ряд сходится в случае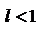 
;
ряд расходится в случае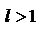 
;
3) в случае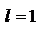 
ответа о сходимости или расходимости ряда теорема не дает.
11 Радикальный признак Коши.
Если для ряда с положительными членами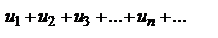 
величина 
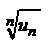имеет конечный предел l при 
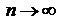, то есть 
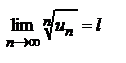, то
в случае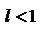 
ряд сходится;
в случае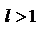 
ряд расходится;
3) в случае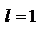 
ответа о сходимости или расходимости ряда теорема не дает.
Доказательство:
Пусть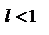 
. Рассмотрим число q, удовлетворяющее соотношению 
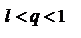. Начиная с некоторого номера n=N будет иметь место соотношение 
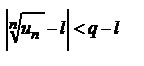. Отсюда следует, что 
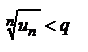или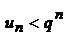 
для всех 
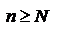. Рассмотрим теперь два ряда: 
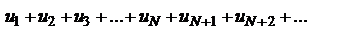(1) и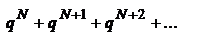 
(2). Ряд 2 сходится, так как его члены образуют убывающую геометрическую прогрессию. Члены ряда 1, начиная с 
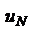, меньше членов ряда 2. Следовательно, ряд 1 сходится.
Пусть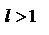 
. Тогда, начиная с некоторого номера n=N будем иметь 
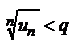или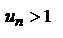 
. Но если все члены рассматриваемого ряда, начиная с 
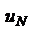, больше 1, то ряд расходится, так как его общий член не стремится к нулю.
12. Знакопеременные ряды. Абсолютная и условная сходимость.
