Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные

Теорема1. Если знакопеременный ряд 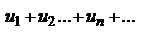таков, что ряд, составленный из абсолютных величин его членов 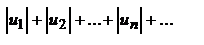сходится, то и данный знакопеременный ряд также сходится.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов расходится, то данный ряд называется условно или не абсолютно сходящимся рядом.

13 Теорема Лейбница:

Если в з/ч ряде абсолютные величины членов ряда убывают, и общий их член →0, то ряд сходится, причем его сумма по общей величине меньше первого члена ряда, а остаток ряда по модулю меньше первого из отбрасываемых членов. Док-во. Рассмотрим частичную сумму ряда с номером 2N: 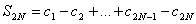и заметим, что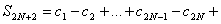 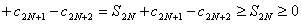, т.к. по условию 1 имеем нер-во: . .

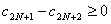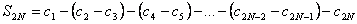14. Знакочередующиеся ряды. Теорема Лейбница.

Теорема Лейбница:

Если в знакочередующемся ряду 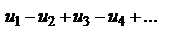, где 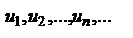положительны, члены таковы, что 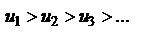и 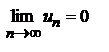, то ряд сходится, его сумма положительна и не превосходит первого члена.

Доказательство: Рассмотрим сумму 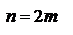первых членов ряда. 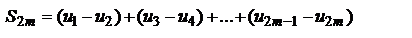По условию 1 выражение в каждой скобке положительно. Следовательно, сумма 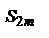положительна и возрастает с возрастанием m. Запишем теперь эту же сумму так:

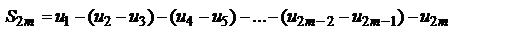По условию 1 каждая из скобок положительна. Поэтому в результате вычитания этих скобок из 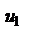мы получим число, меньшее 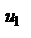. Таким образом, мы установили, что 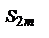при возрастании m возрастает и ограничена сверху. Отсюда следует, что 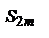имеет предел S

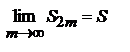, причем 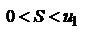. Однако сходимость еще не доказана. Мы доказали только, что последовательность четных частичных сумм имеет пределом число S. Докажем теперь, что нечетные частичные суммы также стремятся к пределу S. Рассмотрим для этого сумму 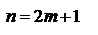первых членов исходного ряда. 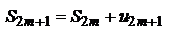. Так как по условию 2 теоремы 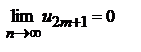, то следовательно 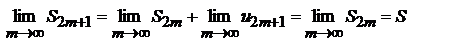Тем самым мы доказали, что 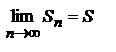как при четном n, так и при нечетном. Следовательно, исходный ряд сходится.