Если указанный интеграл расходится, то расходится и исходный ряд

Доказательство:

1) Предположим, что интеграл 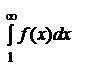сходится, то есть имеет конечное значение. Так как 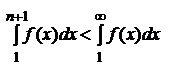, то 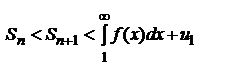, то есть частичная сумма Sn остается ограниченной при всех значениях n. Но при увеличении n она возрастает, так как все члены u_n положительны. Следовательно, Sn при 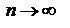имеет конечный придел 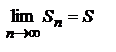, то есть ряд сходится.

2) Предположим далее, что 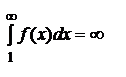. Это значит, что 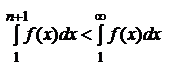неограниченно возрастает при возрастании n. Но тогда Sn также неограниченно возрастает при возрастании n, то есть ряд расходится.

8. Признаки сравнения. Признак Даламбера.

Обычный признак сравнения.