Предельный признак сравнения

Если сущ-ет limU_n/V_n=L, но L¹0,¥ при n®¥, то ряды ведут себя одинаково.

10. Признаки сравнения. Признак Даламбера.

Обычный признак сравнения.

Пусть имеем два ряда с положительными членами

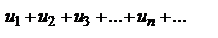(1) и 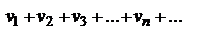(2), для которых выполняется условие: 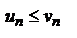. Тогда из сходимости ряда 2 следует сходимость ряда 1;

Из расходимости ряда 1 следует расходимость ряда 2.

Предельный признак сравнения.

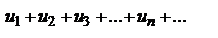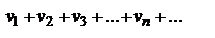Имеем два ряда (1) и (2).

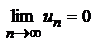. Если L существует, то оба ряда сходятся одновременно.

Пусть ряд 2 сходится, тогда по обычному признаку сравнения сходится и ряд 1.

Имеем ряд :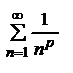

1) 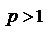ряд сходится

2) 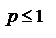ряд расходится.