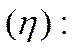Дисперсия – это показатель вариации, выражающий средний квадрат отклонений вариантов от средней величины. В зависимости от образующих вариацию факторов различают общую, межгрупповую и внутригрупповую дисперсию.
1.Общая дисперсия 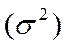 - образуется под вилянием совокупного действия всех факторов на изучаемое явление. Общая дисперсия определяется по формулам:
- образуется под вилянием совокупного действия всех факторов на изучаемое явление. Общая дисперсия определяется по формулам:
а) невзвешенной - 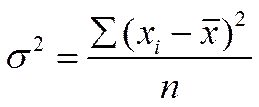 ;
;
б) взвешенной - 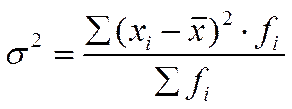 .
.
2.Межгрупповая дисперсия 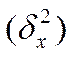 - характеризует влияние на колеблемость изучаемого признака лишь группировочного признака.Она представляет собой средний квадрат отклонения групповых средних
- характеризует влияние на колеблемость изучаемого признака лишь группировочного признака.Она представляет собой средний квадрат отклонения групповых средних 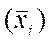 от общей средней
от общей средней 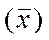 :
:
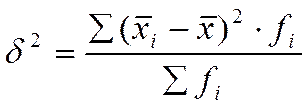 .
.
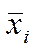 - групповые средние;
- групповые средние;
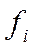 - число единиц в группах;
- число единиц в группах;
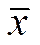 - общая средняя.
- общая средняя.
3.Внутригрупповая дисперсия 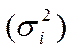 - характеризует в группах статистической совокупности влияние на колеблемость изучаемого признака прочих факторов, кроме группировочного. Это вариация, которая осталась в группах после расчленения статистической совокупности на однородные группы.
- характеризует в группах статистической совокупности влияние на колеблемость изучаемого признака прочих факторов, кроме группировочного. Это вариация, которая осталась в группах после расчленения статистической совокупности на однородные группы.
Частные или внутригрупповые дисперсии – это дисперсии, вычисленные для каждой группы совокупности. Служат они для характеристики рассеяния признака в каждой группе:
а) невзвешенные - 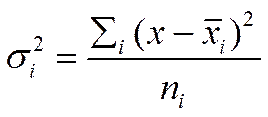 ;
;
б) взвешенные –
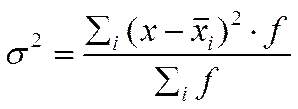 ,
,
где 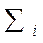 - суммирование по каждой группе.
- суммирование по каждой группе.
Обобщающей характеристикой внутри-групповой дисперсии является средняя внутригрупповая дисперсия 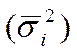 :
:
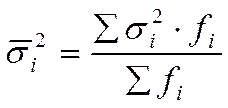 .
.
Между общей, межгрупповой и средней внутригрупповой дисперсией имеется зависимость, которая выражается формулой:
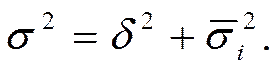
4.Эмпирический коэффициент детерминации 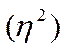 :
:
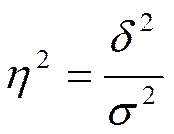 .
.
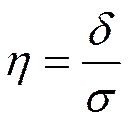 .
.
Показывает тесноту связи между группировочным и результативным признаком.
6. Дисперсия альтернативного признака
Среди варьирующих признаков, которые изучает статистика, имеются признаки, вариация которых проявляется в том, что у одних единиц совокупности они встречаются, а у других нет.
Признаки, которыми обладают одни единицы и не обладают другие, называются альтернативными.
Колеблемость альтернативного признака измеряется дисперсией 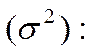
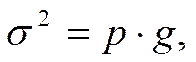
где p – доля вариантов, обладающих данным признаком;
g - доля вариантов, не обладающих данным признаком.
При этом 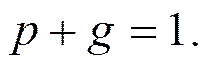
Тогда 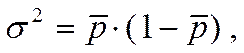
где 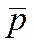 - доля изучаемого признака во всей совокупности, определяемая по формуле:
- доля изучаемого признака во всей совокупности, определяемая по формуле:
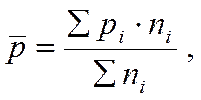
где 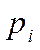 - групповые доли;
- групповые доли;
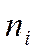 - число единиц в группах.
- число единиц в группах.
Среднее квадратическое отклонение альтернативного признака 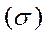 вычисляется по формуле:
вычисляется по формуле:
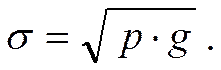
 2015-05-30
2015-05-30 10185
10185