Это определение приспособлено для ситуации с континуальным количеством равновероятных исходов, когда классическое определение не работает.
Говорят, что СЭ удовлетворяет геометрическом распределению если:
1. Исход можно изобразить точками некоторой области 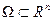 , имеющий конечную меру
, имеющий конечную меру 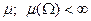 .
.
2. Можно считать, что попадание точки в любые области 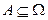 , имеющие одинаковую конечную меру
, имеющие одинаковую конечную меру 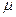 равновозможное и не зависит от формы и расположения
равновозможное и не зависит от формы и расположения 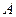 внутри
внутри 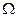 . При этом говорят, что точка бросается наудачу.
. При этом говорят, что точка бросается наудачу.
Согласно геометрическому определению вероятности, вероятность попадания в любую область 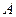 пропорционально ее мере
пропорционально ее мере 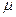 .
.
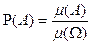 .
.
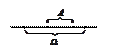 Рассмотрим частные случаи:
Рассмотрим частные случаи:
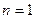 ;
; 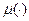 - длина подмножества на числовой прямой
- длина подмножества на числовой прямой 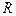 .
.
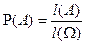

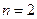 ;
; 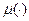 - площадь подмножества на плоскости
- площадь подмножества на плоскости 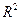 .
.
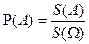
При 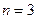 мерой будет являться объем.
мерой будет являться объем.
Из геометрического определения вероятности вытекают свойства:
1. 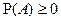 ;
;
2. 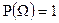 - условие нормировки;
- условие нормировки;
3. 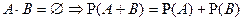 ;
;
Т.к. свойства 1-3 справедливы, то из них вытекают:
4. 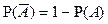 т.к.
т.к. 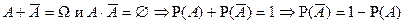 .
.
5. 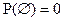 из свойства 4 (
из свойства 4 (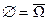 ).
).
6. 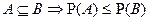 .
. 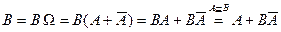 . Покажем несовместность событий
. Покажем несовместность событий 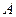 и
и 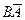 :
: 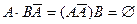 . Тогда
. Тогда 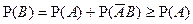 .
.
7. 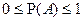 т.к.
т.к. 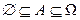 и свойство 6.
и свойство 6.
Пример: Стержень наугад разламывается на 2 части, какова вероятность того, что длины обломков будут отличаться более чем в 2 раза.
Решение: Исход - точка 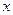 в которой и сломается стержень.
в которой и сломается стержень.
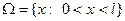 ;
; 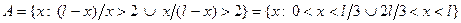 .
.
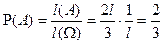 .
.
 2015-05-30
2015-05-30 829
829








