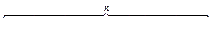Говорят, что СЭ удовлетворяет КОВ, если:
1. 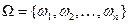
2. Исходы случайного эксперимента равновозможные.
Исходы можно считать равновозможными, если они обладают свойством симметричности относительно условий проведения экспериментов (т.е. ни один исход не имеет предпочтение перед другим).
Пусть 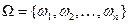 и
и 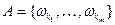 - благоприятствующее событие и
- благоприятствующее событие и 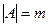 . Согласно КОВ, за
. Согласно КОВ, за 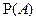 принимают отношение числа исходов, благоприятствующих
принимают отношение числа исходов, благоприятствующих 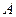 к общему числу исходов:
к общему числу исходов: 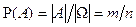 .
.
Свойства, вытекающие из классического определения вероятности:
1. 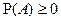 ;
;
2. 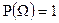 - условие нормировки;
- условие нормировки;
3. 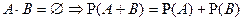 ;
; 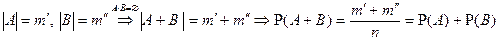 .
.
4. 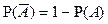 т.к.
т.к. 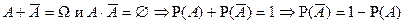 .
.
5. 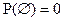 из свойства 4 (
из свойства 4 (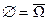 ).
).
6. 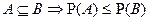 .
. 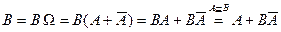 . Покажем несовместность событий
. Покажем несовместность событий 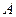 и
и 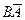 :
: 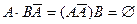 . Тогда
. Тогда 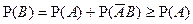 .
.
7. 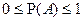 т.к.
т.к. 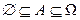 и свойство 6.
и свойство 6.
Рассмотрим урновую схему: В урне содержится 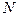 шаров, из которых
шаров, из которых 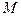 - белых. Наугад из урны извлекается
- белых. Наугад из урны извлекается 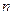 шаров. Какова вероятность того, что среди них окажется ровно
шаров. Какова вероятность того, что среди них окажется ровно 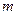 белых?
белых?
|

 Решение: Исход – набор из
Решение: Исход – набор из 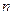 шаров. Общее число исходов
шаров. Общее число исходов 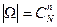 . Число благоприятных исходов:
. Число благоприятных исходов: 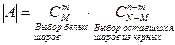 .
. 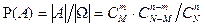 .
.
Пример: В партии из 100 деталей содержится 5 бракованных. Для контроля наугад отбирают 10 деталей. Какова вероятность того, что среди них окажется хотя бы 1 бракованная.
|
|
|
Решение: Рассмотрим событие 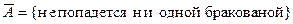 , тогда
, тогда
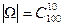 и
и 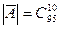 . Получим
. Получим 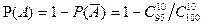 .
.
 2015-05-30
2015-05-30 2056
2056