Аксиоматическое определение вероятности. Вероятностное пространство. Свойства вероятности

Сформулировано в 1933 г. Колмогоровым А.Н.

Опр Класс подмножеств 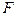множества 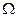называют 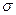-алгеброй, если выполнены условия:

1. ;
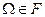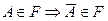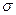2. - -алгебра замкнута относительно перехода к противоположному событию.
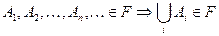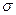3. - -алгебра замкнута относительно операции сложения.

Утверждения 1-3 называются аксиомами 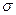-алгебры.

Покажем, что 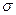-алгебра замкнута относительно произведения и разности:

1. .
2. .

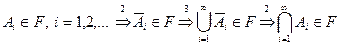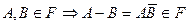Множества 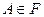и только они называются случайными событиями. Пара 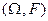, где 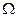- пространство элементарных событий, а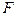 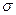-алгебра его подмножеств называется измеримым пространством.

Опр Пусть 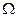- пространство элементарных событий, а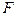 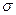-алгебра его подмножеств. Функция 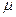, отображающая 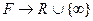(в вещественную прямую), называется мерой на измеримом пространстве 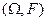, если она удовлетворяет условиям:

1. ;
2. .

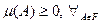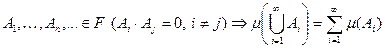Последние 2 утверждения называются аксиомами меры (аксиома неотрицательности и аддитивности). Мера 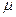отображающая 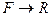называется нормированной мерой на измеримом пространстве 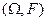, если .

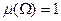Пусть 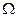- пространство элементарных событий, а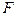 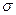-алгебра его подмножеств. Вероятностью или вероятностной мерой на измеримом пространстве 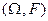называется функция 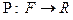, удовлетворяющая следующей системе аксиом:

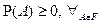1. (аксиома неотрицательности);
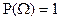2. (аксиома нормированности);
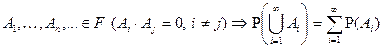3. (аксиома счетной аддитивности).

Тройка 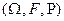называется вероятностным пространством.

Теорема Аксиома счетной аддитивности (3) эквивалентна 2-м аксиомам:

3*. Аксиома конечной аддитивности .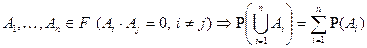

4. Если 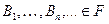- последовательность событий, удовлетворяющая:

1. ;

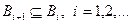2. .

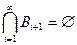то 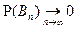. Такая последовательность называется убывающей последовательностью событий.

Свойства вероятности:

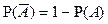1. т.к. .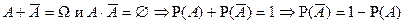

2. 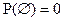из свойства 1 ().

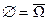3. 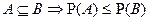. . 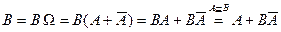Покажем несовместность событи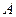й и 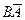: 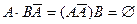. Тогда .

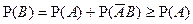4. 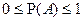т.к. 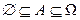и свойство 3.

5. Теорема сложения вероятностей: .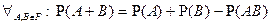

Доказательство: 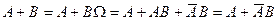, 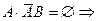по аксиоме аддитивности:

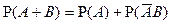(1).

Представим 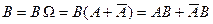и 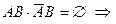несовместимы 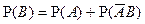(2).

.

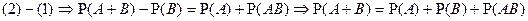6. Если 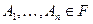образует ПГС, то 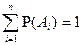. Утверждение следует из свойства вероятности 3* и 4.