Информация о наступлении одного события может повлечь изменение шансов появления другого.
 Пусть
Пусть 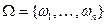 - конечное пространство равновозможных элементарных исходов.
- конечное пространство равновозможных элементарных исходов. 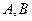 – некоторые события. Вероятность, того, что событие
– некоторые события. Вероятность, того, что событие 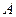 произойдет равно
произойдет равно 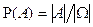 , если же известно, что событие
, если же известно, что событие 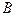 произошло, то следует выбрать новое вероятностное пространство
произошло, то следует выбрать новое вероятностное пространство 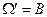 , и рассматривать событие
, и рассматривать событие 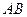 . Т.о. вероятность того, что событие
. Т.о. вероятность того, что событие 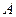 произойдет, при условии, что
произойдет, при условии, что 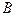 уже произошло:
уже произошло:
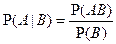 .
.
Полученное выражение для 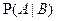 и принимается за определение условной вероятности.
и принимается за определение условной вероятности.
Опр Пусть 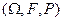 - некоторое вероятностное пространство
- некоторое вероятностное пространство 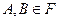 ,
, 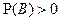 . Условной вероятностью события
. Условной вероятностью события 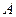 , при условии, что
, при условии, что 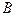 уже произошло называется величина:
уже произошло называется величина: 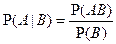 .
.
Условная вероятность 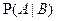 при фиксированном
при фиксированном 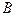 удовлетворяет всем аксиомам вероятности, а именно:
удовлетворяет всем аксиомам вероятности, а именно:
-
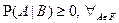 (аксиома неотрицательности);
(аксиома неотрицательности); -
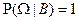 (аксиома нормированности);
(аксиома нормированности); -
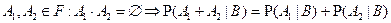 .
.
Т.к. 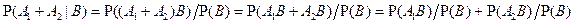 .
.
Из справедливости этих аксиом, можно утверждать, что условная вероятность обладает всеми свойствами вероятностей.
Из определения условной вероятности вытекает правило умножения вероятностей:
|
|
|
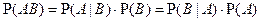 ,
, 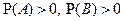 .
.
Обобщим правило умножения на случай счетного числа событий (теорема умножения):
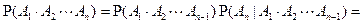
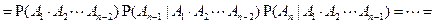
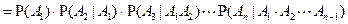 .
.
 2015-05-30
2015-05-30 2493
2493
