Пусть 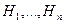 - ПГС, причем
- ПГС, причем 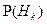 и
и 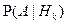 - известны
- известны 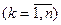 . Найдем
. Найдем 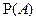 .
.
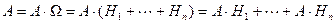 - слагаемые справа попарно несовместны
- слагаемые справа попарно несовместны 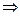 с учетом аддитивности вероятности и правилом умножения получим:
с учетом аддитивности вероятности и правилом умножения получим:
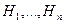 - гипотезы, отметим, что
- гипотезы, отметим, что 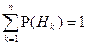 , т.к. гипотезы составляют ПГС.
, т.к. гипотезы составляют ПГС.
Пусть с экспериментом связано 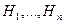 - гипотез, вероятности которых известны, также известно, что гипотеза
- гипотез, вероятности которых известны, также известно, что гипотеза 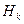 сообщает событию
сообщает событию 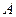 вероятность
вероятность 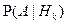 . Предположим, что после проведение эксперимента событие
. Предположим, что после проведение эксперимента событие 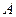 произошло. Этот факт приводит к переоценке первоначальных вероятностей гипотез
произошло. Этот факт приводит к переоценке первоначальных вероятностей гипотез 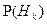 .
.
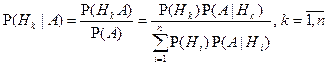 - формула Байеса, где
- формула Байеса, где
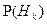 - априорные вероятности гипотез;
- априорные вероятности гипотез;
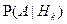 - апостериорные вероятности гипотез.
- апостериорные вероятности гипотез.
Пример:
По каналу связи с помехами передаются бинарные символы (0 и 1). Вероятность искажения символа в канале равна 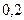 . Вероятности символов на входе каналов:
. Вероятности символов на входе каналов: 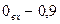 и
и 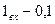 . На выходе принят сигнал соответствующий
. На выходе принят сигнал соответствующий 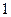 . Какова вероятность того, что на входе также была
. Какова вероятность того, что на входе также была 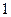 .
.
Решение: 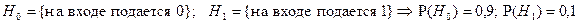
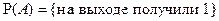 . Т.о. необходимо найти апостериорную вероятность
. Т.о. необходимо найти апостериорную вероятность 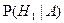 .
.
Очевидно, 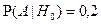 и
и 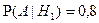 . По формуле Байеса получим:
. По формуле Байеса получим:
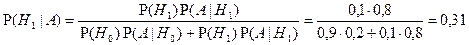 ;
; 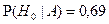 .
.
 2015-05-30
2015-05-30 1088
1088

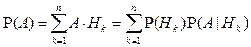 -
-