Случайная величина (СВ) (интуитивное определение) – числовая функция, значение которой заранее определить невозможно, т.е. функция зависящая от случайного исхода и принимающая свои значения с некоторыми вероятностями. 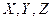 - обозначение случайных величин.
- обозначение случайных величин. 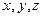 - значения СВ.
- значения СВ.
Формальное определение СВ: Пусть имеется случайный эксперимент и задано вероятностное пространство 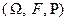 .
. 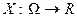 - называется случайной величиной, если
- называется случайной величиной, если
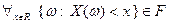 .
. 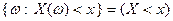 является событием
является событием 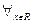 .
.
Говорят, что функция 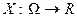 является
является 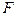 - измеримой (измеримой относительно
- измеримой (измеримой относительно 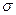 -алгебры
-алгебры 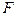 ), если множество
), если множество 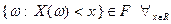 . Т.о. СВ есть
. Т.о. СВ есть 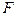 - измеримая функция ставящая в соответствие каждому элементарному исходу
- измеримая функция ставящая в соответствие каждому элементарному исходу 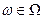 вещественное число
вещественное число 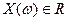 .
.
Из определения СВ и 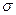 -алгебры следует, что событиями являются также подмножества, связанные со СВ
-алгебры следует, что событиями являются также подмножества, связанные со СВ 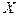 :
: 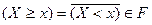 ;
; 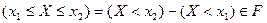 ;
;
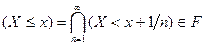 ;
; 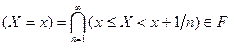 , и любые другие подмножества, получающиеся из данных путем выполнения конечного или счетного числа операций. Другими словами, попадание СВ в Борелевское множество на числовой прямой является событием:
, и любые другие подмножества, получающиеся из данных путем выполнения конечного или счетного числа операций. Другими словами, попадание СВ в Борелевское множество на числовой прямой является событием:
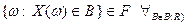 .
.
Для определения вероятностей любых событий, связанных со СВ и делать это аналогичным способом для всех величин в ТВ вводится понятие функции распределения (ФР).
|
|
|
ФР -я СВ 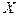 называется функция
называется функция 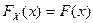 , отображающая
, отображающая 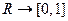 , при каждом
, при каждом 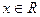 , определяемая равенством:
, определяемая равенством: 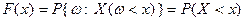 . Геометрически ФР в точке
. Геометрически ФР в точке 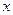 означает вероятность попадания СВ
означает вероятность попадания СВ 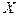 левее заданной точки
левее заданной точки 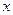 .
.
Свойства ФР:
1. 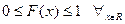 - т.к. ФР является вероятностью.
- т.к. ФР является вероятностью.
2. ФР – неубывающая функция: 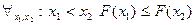 .
.
Доказательство: 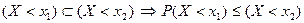 .
.
3. 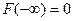 и
и 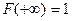 .
.
Замечание: Если 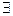 предел
предел 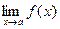 , то для произвольной последовательности
, то для произвольной последовательности 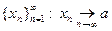 справедливо
справедливо 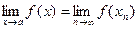 .
.
Доказательство: Существование предела вытекает из ограниченности и монотонности. В соответствии с замечанием к доказательству, что для того чтобы доказать, что 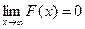 достаточно показать, что
достаточно показать, что 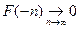 . Пусть
. Пусть 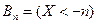 , тогда
, тогда 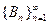 обладает свойствами:
обладает свойствами:
1. 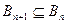 ; (*)
; (*)
2. 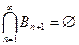 . (**)
. (**)
Т.о. в соответствии с аксиомой непрерывности вероятности, с учетом того, что 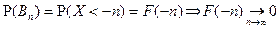 .
.
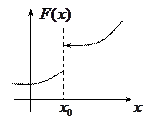 Для доказательства 2-го утверждения достаточно показать, что
Для доказательства 2-го утверждения достаточно показать, что 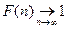 или
или 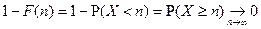 . Рассмотрим
. Рассмотрим 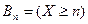 , последовательность
, последовательность 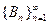 удовлетворяет свойствам (*) и (**), а следовательно является убывающей. Аналогично получим, что
удовлетворяет свойствам (*) и (**), а следовательно является убывающей. Аналогично получим, что 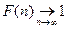 .
.
4. ФР является функцией непрерывной слева: 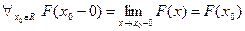 .
.
Замечание: Геометрически свойство означает, что в точках разрыва ФР принимает нижнее (меньшее) значение (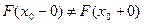 ).
).
Доказательство: докажем, что 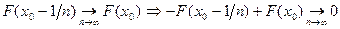 или
или
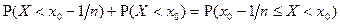 . Пусть
. Пусть 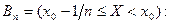 тогда для
тогда для 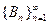 выполняются свойства (*) и (**)
выполняются свойства (*) и (**) 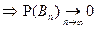 . Т.о.
. Т.о. 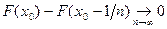 .
.
Свойства 1-3 полностью описывают класс ФР (т.е. если функция 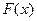 удовлетворяет свойствам 1-3, то это ФР некоторой СВ).
удовлетворяет свойствам 1-3, то это ФР некоторой СВ).
5. 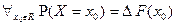 , где
, где 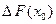 - величина скачка ФР в точке
- величина скачка ФР в точке 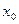 .
.
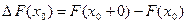 .
.
Следствие: Если ФР 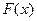 является непрерывной в т.
является непрерывной в т. 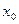 то
то 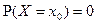 .
.
Доказательство: 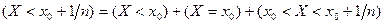 . Событие справа попарно несовместно
. Событие справа попарно несовместно 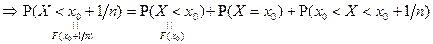 .
.
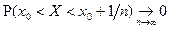 , т.к.
, т.к. 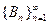 ,
, 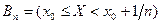 подчиняется свойствам (*) и (**). Т.о.
подчиняется свойствам (*) и (**). Т.о. 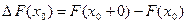 .
.
6. 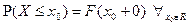 .
.
Доказательство: 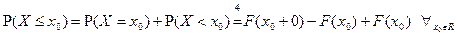 .
.
7. 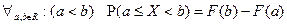 .
.
Доказательство: 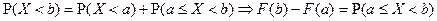 .
.
8. 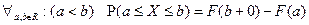 ;
;
9. 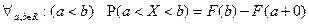 ;
;
10. 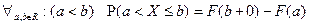 .
.
 2015-05-30
2015-05-30 1979
1979
