Опр НСВ – случайная величина 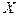 - определенная на вероятностном пространстве
- определенная на вероятностном пространстве 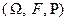 называется непрерывной, если ее функция распределения
называется непрерывной, если ее функция распределения 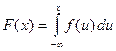 (*).
(*).
Функция 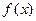 называется плотностью распределения вероятностей (ПВ) НСВ
называется плотностью распределения вероятностей (ПВ) НСВ 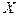 .
.
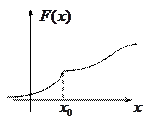 Из определения НСВ напрямую вытекают свойства ФР НСВ:
Из определения НСВ напрямую вытекают свойства ФР НСВ:
1. 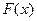 - непрерывная
- непрерывная 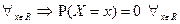 . (следует из непрерывности интегрирования с переменным верхним пределом, при этом
. (следует из непрерывности интегрирования с переменным верхним пределом, при этом 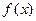 необязательно непрерывна).
необязательно непрерывна).
2. В точках непрерывности 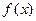 ф-ция распределения
ф-ция распределения 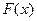 является дифференцируемой и
является дифференцируемой и 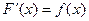 (**) (следует из свойства 1 и свойства интегрирования с переменным верхним пределом). В точках, где непрерывности
(**) (следует из свойства 1 и свойства интегрирования с переменным верхним пределом). В точках, где непрерывности 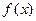 нет ФР имеет излом.
нет ФР имеет излом.
Замечание: Представление (*) задает плотность вероятностей неоднозначно, поскольку изменение 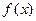 на любом множестве меры 0, не изменит этого представления. Поэтому говорят, что ФР НСВ является дифференцируемой почти всюду и
на любом множестве меры 0, не изменит этого представления. Поэтому говорят, что ФР НСВ является дифференцируемой почти всюду и 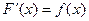 для почти всех
для почти всех 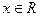 .
.
Из (**) и определения производной следует: 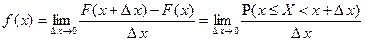 .
.
Т.о. с физической точки зрения можно интерпретировать 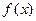 , как массу, приходящуюся на отрезок
, как массу, приходящуюся на отрезок 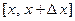 . Это оправдывает понятие
. Это оправдывает понятие 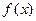 как плотности.
как плотности.
Несмотря на то, что (*) и (**) устанавливают взаимнооднозначное соответствие между ПВ и ФР, но ПВ является более наглядной вероятностной характеристикой НСВ. ПВ также называют законом распределения НСВ.
Свойства плотности вероятности:
1. 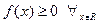 (почти всюду) т.к. ФР неубывающая функция.
(почти всюду) т.к. ФР неубывающая функция.
2. 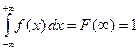 - условие нормировки.
- условие нормировки.
3. 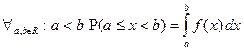 .
.
Т.к. 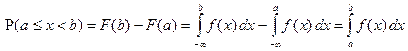 .
.
При НСВ 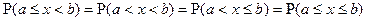 т.к.
т.к. 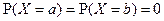 .
.
Свойства 1 и 2 полностью описывают класс ПВ (если 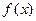 удовлетворяет свойствам 1 и 2, то
удовлетворяет свойствам 1 и 2, то 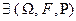 и НСВ, плотностью которой она является).
и НСВ, плотностью которой она является).
 2015-05-30
2015-05-30 2704
2704
