2015-05-30
727
Рассмотрим простейшую последовательность независимых испытаний, в каждом из которых возможно только 2 исхода: успех -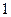 
и неуспех - 
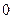. Такая схема независимых испытаний называется схемой Бернулли. Пусть 
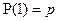и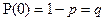 
.
Пространство элементарных событий после проведения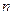 
испытаний по схеме Бернулли имеет вид: 
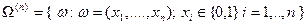. При этом 
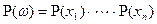, где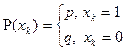 
. Т.о. 
.
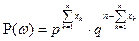При рассмотрении схемы Бернулли обычно интересуются событиями вида:
, 
.
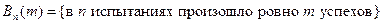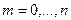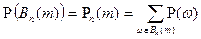, где 
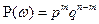и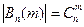 
.
Откуда получим формулу Бернулли:
.
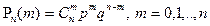Поскольку события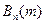 
при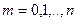 
образуют ПГС, то
.
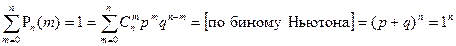Рассмотрим отношение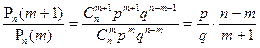 
. Откуда видно, что
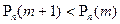, если 
;
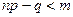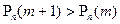, если 
;
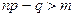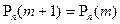, если 
.
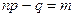Обозначим за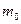 
- число успехов при котором функция 
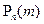достигает максимума (наивероятнейшее число успехов). Тогда 
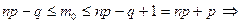если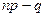 
- не целое, то 
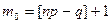. А если 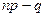- целое, то существует 2 наивероятнейших числа успехов 
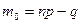и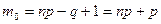 
. Если 
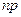- целое число, то, очевидно, 
.
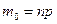При больших 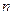и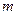 
вычисление 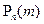очень трудоемко, для этого используются приближенные формулы, основанные на предельных теоремах Пуассона и Муавра-Лапласа.
