Начальным моментом (НМ) 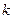 -го порядка СВ
-го порядка СВ 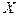 называется МО
называется МО 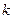 -ой степени этой СВ.
-ой степени этой СВ.
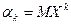 , если МО существует. (*)
, если МО существует. (*)
Обычно рассматривается НМ положительного и целого порядка: 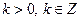 ;
;
Например: 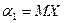 и
и 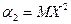 .
.
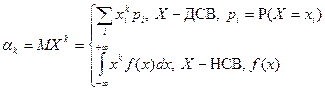
Центральным моментом 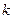 - го порядка
- го порядка 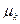 СВ
СВ 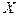 называется МО,
называется МО, 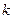 - ой степени, отклонения этой СВ от ее МО:
- ой степени, отклонения этой СВ от ее МО: 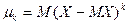 .
.
СВ 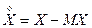 называется центрированной СВ (ЦСВ), т.к.
называется центрированной СВ (ЦСВ), т.к. 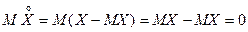 .
.
Т.о. 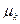 СВ
СВ 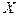 , есть начальный момент
, есть начальный момент 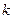 - го порядка ЦСВ:
- го порядка ЦСВ: 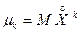 .
.
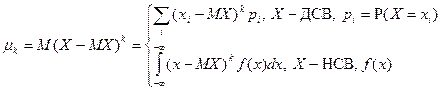 .
.
Особую роль на практике играет 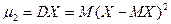 (**), называемый дисперсией Д (МО квадрата отклонения СВ от своего МО). Д характеризует степень разброса СВ относительно ее МО (степень рассеянья).
(**), называемый дисперсией Д (МО квадрата отклонения СВ от своего МО). Д характеризует степень разброса СВ относительно ее МО (степень рассеянья).
В механической интерпретации Д есть момент инерции, распределения единицы массы относительно центра масс.
На ряду с формулой (**) используется также:
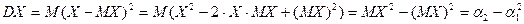
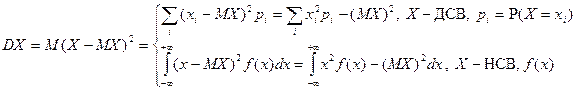 .
.
Свойства Д:
1. 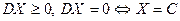 п.н.
п.н.
Доказательство: 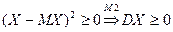 . Если
. Если 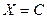 , то
, то 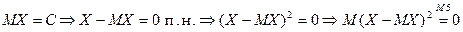 . И в обратную сторону:
. И в обратную сторону:
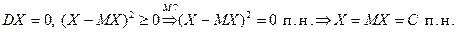
2. 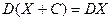 . Дисперсия не изменяется при добавлении к СВ константы.
. Дисперсия не изменяется при добавлении к СВ константы.
Доказательство: 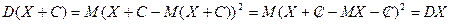 .
.
3. 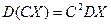 , где
, где 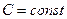 .
.
Доказательство: 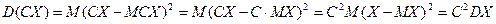 .
.
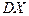 имеет размерность квадрата СВ. Характеристикой рассеянья, имеющей размерность самой СВ является средне-квадратичное отклонение
имеет размерность квадрата СВ. Характеристикой рассеянья, имеющей размерность самой СВ является средне-квадратичное отклонение 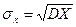 (
(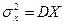 ).
).
|
|
|
 2015-05-30
2015-05-30 724
724








