2015-05-30
334
При расчете средней арифметической для интервального вариационного ряда сначала определяют среднюю для каждого интервала, как полусумму верхней и нижней границ, а затем — среднюю всего ряда. В случае открытых интервалов значение нижнего или верхнего интервала определяется по величине интервалов, примыкающих к ним.
Пример 3. Определить средний возраст студентов вечернего отделения.
Возраст студенов,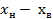 
| Число студентов,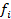 
| Среднее значение интервала,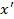 
| Произведение середины интервала (возраст) на число студентов,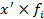 
|
| до 20 | 65 | (18 + 20) / 2 =19 18 в данном случае граница нижнего интервала. Вычисляется как 20 — (22-20) | 1235 |
| 20 — 22 | 125 | (20 + 22) / 2 = 21 | 2625 |
| 22 — 26 | 190 | (22 + 26) / 2 = 24 | 4560 |
| 26 — 30 | 80 | (26 + 30) / 2 = 28 | 2240 |
| 30 и более | 40 | (30 + 34) / 2 = 32 | 1280 |
| Итого | 500 | 11940 |
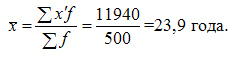
Средние, вычисляемые из интервальных рядов являются менее точными, чем если бы по этим же данным рассчитывали простые средние.
